If √1+x2sinθ=x, Prove that tan2θ+cot2θ=x2+1x2Solution in Tamil
The correct Answer is:∴tan2θ+cot2θ=x2+1x2
Step by step video, text & image solution for If sqrt(1+x^(2))sintheta=x," Prove that "tan^(2)theta+cot^(2)theta=x^(2)+(1)/(x^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Mensuration
9 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Co-ordinate Geometry
6 Videos
- ARITHMETIC PROGRESSION BOOK - CHETAN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - ASSIGENMENT -3
10 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
Similar Questions
A tin maker converts a cubical metalic box into 10 cylindrical tins. Side of the cube is 50 cm and radius of the cylindrical is 7cm. Find the height of each cylinder so made if the wastage incurred was 12%. (π=227)
View SolutionIf A(−14,−10),B(6,−2) is given, find the co-ordinates of the points which divide segment AB into four equal parts.
View SolutionWhat is the common difference (d) of the A.P. 2,-2,-6,-10….. ?
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.
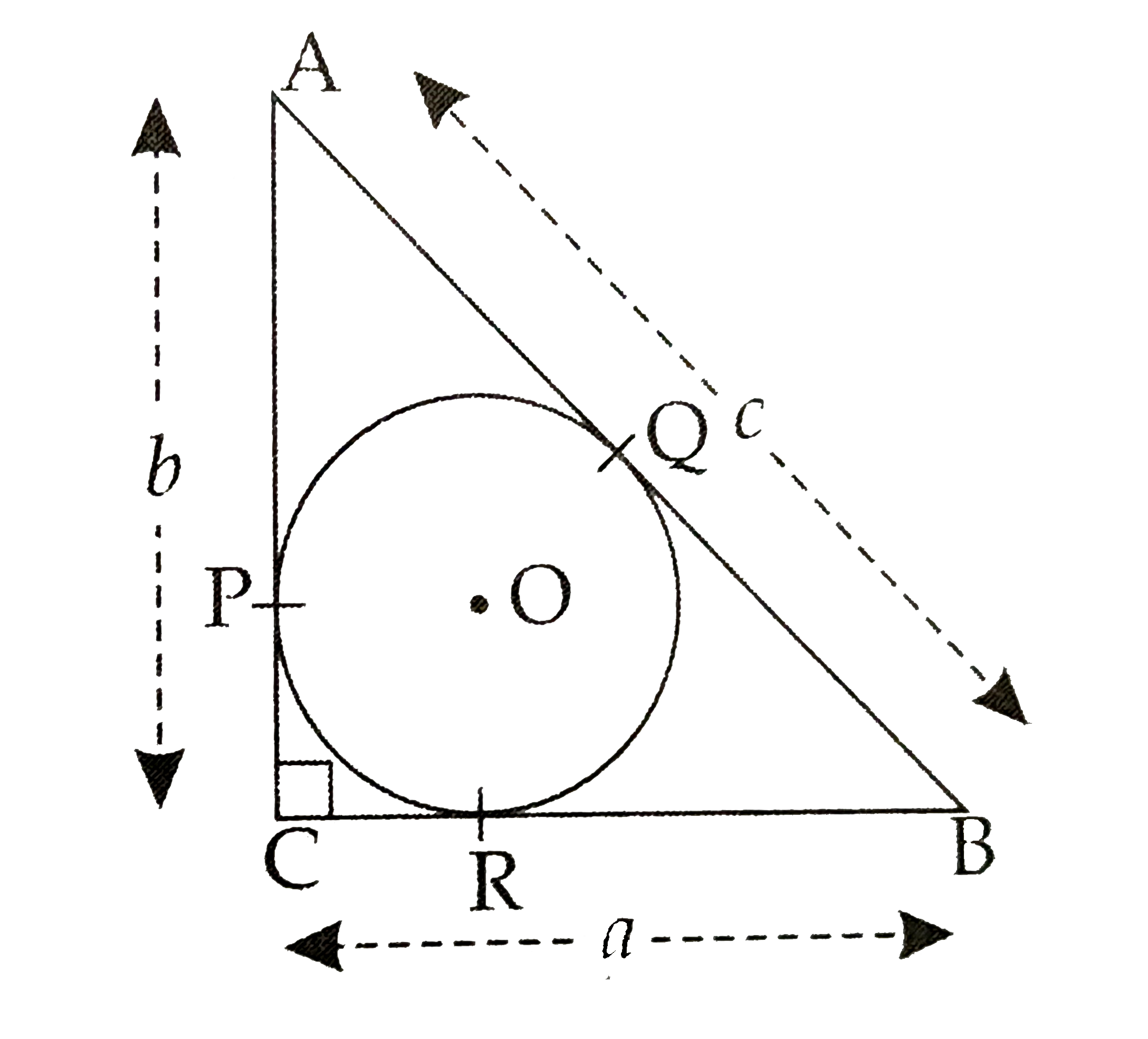
View SolutionProve: 1+tan2θ1+cot2θ=(1−tanθ1−cotθ)2=tan2θ
View SolutionProve that: √1−sinθ1+sinθ=secθ−tanθwhen (−π2)<θ<π2 and −secθ+tanθ when π2<θ<3π2
View SolutionProve that : tan2θ1+tan2θ+cot2θ1+cot2θ=1
View Solutionयदि tanθ+secθ=x,सिद्ध करें कि sinθ=x2−1x2+1
View Solutionसिद्ध कीजिए कि 12sin−1x=cot−1[1+√1−x2sinθ]
View Solutionसिद्ध कीजिए कि : tan2θ1+tan2θ+cot2θ1+cot2θ=1
View Solutionयदि f(x)=x21−x2, तो सिद्ध कीजिए -
f(sinθ)=tan2θ.
View SolutionIf tan−1(√1+x2−√1−x2√1+x2+√1−x2)=θ, then prove that, sin2θ=x2.
View Solutiontan−1(√1+x2−√1−x2√1+x2+√1−x2)=θ হলে প্রমাণ করো যে, sin2θ=x2
View SolutionIf tanθ+secθ=x show that 2 tan θ=x−1x,2secθ=x+1x. Hence show that sinθ=x2−1x2+1
View SolutionIf secθ−tanθ=x, show that
secθ=12(x+1x) and tanθ=12(1x−x).
View Solution
