If 9∑i=1(xi−5)=9 and 9∑i=1(xi−5)2=45. The standard deviation of the observations x1,x2,………,x9 is …………. Solution in Gujrati
9
4
2
3
The correct Answer is:B
Step by step video, text & image solution for If sum_(i=1)^9 (x_i - 5) = 9 and sum_(i=1)^9 (x_i - 5)^2 = 45. The standard deviation of the observations x_1, x_2,………,x_9 is …………. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK
19 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - NCERT EXEMPLAR PROBLEMS (SHORT ANSWER TYPE QUESTIONS)
23 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - TEXTBOOK BASED MCQS
19 Videos
- SETSBOOK - KUMAR PRAKASHANCHAPTER - SETSEXERCISE - QUESTION OF MODULE
28 Videos
- STRAIGHT LINESBOOK - KUMAR PRAKASHANCHAPTER - STRAIGHT LINESEXERCISE - Question of Module (Knowledge Test :)
18 Videos
Similar Questions
Find the mean and variance for each of the data :
6,7,10,12,13,4,8,12
View SolutionFind the mean deviation about the mean of the distribution:
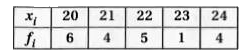
View SolutionThe sum of 20 observations of the deviation from 30 is 20. Their mean is
View SolutionA{x∈R∣x2+3=0} is a set of………type.
View SolutionFind distance between the points A(3,4)andB(−4,3).
View SolutionIf x1,x2,.......,xn are n values of a variable X such that n∑i=1(xi−2)=110 and n∑i=1(xi−5)=20. Find the value of n and the mean.
View SolutionIf 9∑i=1(xi−5)=9and9∑i=1(xi−5)2=45 then the standard deviation of the 9 items x1,x2,.....,x9 is
View SolutionFor observations xi given 10∑i=1(Xi−5)=10 and 10∑i=1(Xi−5)2=40 If mean and variance of observations (x1−3),(x2−3),(x3−3).........(x10−3) is λ & μ respectively then ordered pair (λ,μ) is
View SolutionIf n∑i=1(xi−a)=n and n∑i=1(xi−a)2=na then the standard deviation of variate xi
View Solutionयदि 9∑i=1(xi−5)=9 तथा 9∑i=1(xi−5)2=45 है, तब 9 अवयवों x1,x2,…,x9 का मानक विचलन है
View SolutionIf 9∑i=1(xi−5)=9and9∑i=1(xi−5)2=45, then the standard deviation of the 9 items x1,x2,......,x9 is
View Solutionयदि 9∑i=1(xi−5)=9 तथा 9∑i=1(xi−5)2=45 है, तो 9 प्रेक्षणों x1,x2,….x9 का मानक विचलन है।
View SolutionIf 9∑i=1(xi−5) and∑–––––(i=1)9(xi−5)2=45, then the standard deviation of the 9 items x1,x2,..,x9 is
View SolutionIf x1,x2,.......,xn are n values of a variable X such that n∑i=1(xi−2)=110 and sum_(i=1)^n(x_i-5) =20. Find the value of n and the mean.
View Solutionx1,x2,x3,……….,xn are n observations . n∑i=1(xi−2)=100 and n∑i=1(xi−5)=20 then mean ¯x = …….
View Solution
