If the 13 letter words (need no be meaningful) are to be formed using the letters from the word "MEDITERRANEAN" such that the first letter is R and the fourth letter is, E, then the total number of such words, is
11!(2!)3
59
110
56
To solve the problem, we need to find the total number of 13-letter words that can be formed using the letters from the word "MEDITERRANEAN" with the conditions that the first letter is 'R' and the fourth letter is 'E'.
1. Identify the Letters in "MEDITERRANEAN":
The letters in "MEDITERRANEAN" are:
- M: 1
- E: 2
- D: 1
- I: 1
- T: 1
- R: 2
- A: 2
- N: 2
Total letters = 13.
2. Fix the Positions:
According to the problem, we need to fix the first letter as 'R' and the fourth letter as 'E'. Therefore, we have:
- Position 1: R
- Position 4: E
This means we have used one 'R' and one 'E' from the available letters.
3. Count Remaining Letters:
After fixing 'R' and 'E', the remaining letters are:
- M: 1
- E: 1 (since we used one 'E')
- D: 1
- I: 1
- T: 1
- R: 1 (since we used one 'R')
- A: 2
- N: 2
Total remaining letters = 11.
4. Calculate the Arrangements:
We need to arrange the remaining 11 letters. The number of arrangements of these letters can be calculated using the formula for permutations of multiset:
Number of arrangements=n!p1!⋅p2!⋯pk!
where n is the total number of items to arrange, and pi are the frequencies of the repeating items.
In our case, the frequencies of the remaining letters are:
- E: 1
- D: 1
- I: 1
- T: 1
- R: 1
- M: 1
- A: 2
- N: 2
Thus, we have:
Number of arrangements=11!2!⋅2!
5. Final Calculation:
Now we can compute the value:
Number of arrangements=11!2!⋅2!
This simplifies to:
=11!4(since 2!⋅2!=4)
Conclusion:
The total number of 13-letter words that can be formed under the given conditions is:
11!4
The letters in "MEDITERRANEAN" are:
- M: 1
- E: 2
- D: 1
- I: 1
- T: 1
- R: 2
- A: 2
- N: 2
According to the problem, we need to fix the first letter as 'R' and the fourth letter as 'E'. Therefore, we have:
- Position 1: R
- Position 4: E
After fixing 'R' and 'E', the remaining letters are:
- M: 1
- E: 1 (since we used one 'E')
- D: 1
- I: 1
- T: 1
- R: 1 (since we used one 'R')
- A: 2
- N: 2
We need to arrange the remaining 11 letters. The number of arrangements of these letters can be calculated using the formula for permutations of multiset:
- E: 1
- D: 1
- I: 1
- T: 1
- R: 1
- M: 1
- A: 2
- N: 2
Now we can compute the value:
The total number of 13-letter words that can be formed under the given conditions is:
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs111videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type9videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test30videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
Similar Questions
How many words can be formed from the letters of the word 'COURTESY' whose first letter is C and the last letter is Y?
View SolutionNo of words formed with the letters of the word 'INDIA' is:
View SolutionHow many 5 letters words can be formed using the letters of the words 'INEFFECTIVE'
View SolutionHow many seven letters words can be formed by using the letters of the word SUCCESS so that
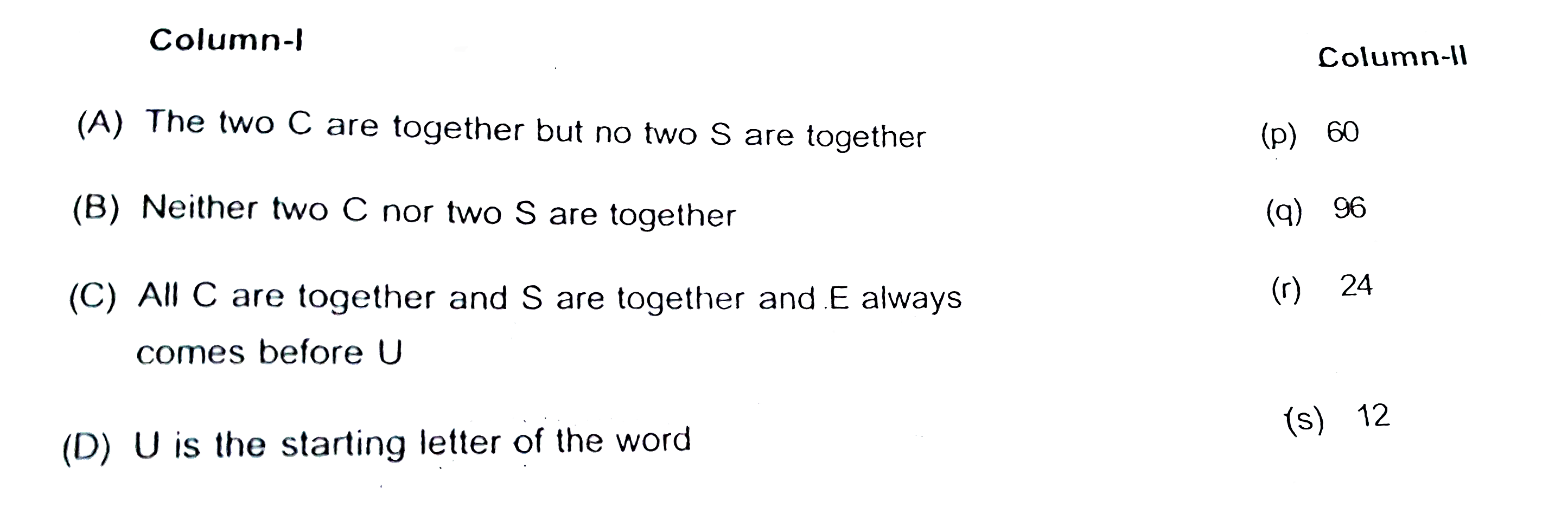 View Solution
View SolutionThe number of 4 letter words (with or without meaning) that can be formed from the letter of the work EXAMINATION is
View SolutionHow many three letter words can be made using the letters of the word ORIENTAL?
View SolutionFind the number of words formed with the letters of the word 'INDIA'.
View SolutionHow many four- letters words can be formed using the letters of the word 'INEFFECTIVE'?
View SolutionWrite the number of words that can be formed out of the letters of the word COMMITTEE.
View SolutionHow many words can be formed from the letters of the word CIRCUMFERENCE.
View Solution

