If the angles and are complementary angles, find
To solve the problem, we need to find the value of x given that the angles (2x−10)∘ and (x−5)∘ are complementary angles. Complementary angles are two angles whose sum is 90∘.
1. Set up the equation for complementary angles:
Since the angles are complementary, we can write the equation:
(2x−10)+(x−5)=90
2. Combine like terms:
Combine the terms on the left side of the equation:
2x−10+x−5=90
This simplifies to:
3x−15=90
3. Isolate the variable x:
To isolate x, first add 15 to both sides of the equation:
3x−15+15=90+15
This simplifies to:
3x=105
4. Solve for x:
Now, divide both sides by 3:
x=1053
This simplifies to:
x=35
Final Answer:
The value of x is 35.
---
Since the angles are complementary, we can write the equation:
(2x−10)+(x−5)=90
Combine the terms on the left side of the equation:
2x−10+x−5=90
This simplifies to:
3x−15=90
To isolate x, first add 15 to both sides of the equation:
3x−15+15=90+15
This simplifies to:
3x=105
Now, divide both sides by 3:
x=1053
This simplifies to:
x=35
The value of x is 35.
Topper's Solved these Questions
Similar Questions
If the angles (2x−10)0 and (x−5)0 are complementary angles, find x.
View SolutionCOMPLEMENTARY ANGLES If the sum of the measures of two angles is 90∘ then the angles are called complementary angles and each is called a complement of the other.
View SolutionTwo complementary angles differ by 12∘ Find them .
View SolutionFind angle 'x' if :
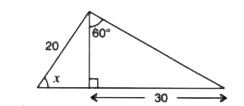 View Solution
View SolutionTwo complementary angles are (x+4)∘and(2x−7)∘, find the value of x
View SolutionIf 2x and 2y are complementary angles and tan(x+2y)=2, then which of the following is (are) correct ?
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1, which make complementary angles with x - axis, is
View SolutionIf two complementary angles differ by 14∘ , find the angles.
View SolutionTwo angles are in the ratio 4:5 Find the angles if they are (i) complementary (ii) supplementary to each other.
View SolutionAngles A and B are complementary and the measure of angle A is twice the measure of angle B. Find the measures of angles A and B
View Solution

