Question

If the angles of a triangle are in the ratio $4:1:1,$
then the ratio of the longest side to the perimeter is
$\sqrt{3}:(2+\sqrt{3})$
(b) $1:6$

$1:2+\sqrt{3}$
(d) $2:3$

Options

A. `sqrt(3):(2+sqrt(3))`
B. `1 : 6`
C. `1:(2+sqrt(3))`
D. `2 : 3`

Answer

A

Explanation

Here , ratio of angles are `4 : 1 : 1`.
`rArr4x+x+x=180^(@)`
`rArrx=30^(@)`
`thereforeangleA=120^(@),angleB=angleC=30^(@)`

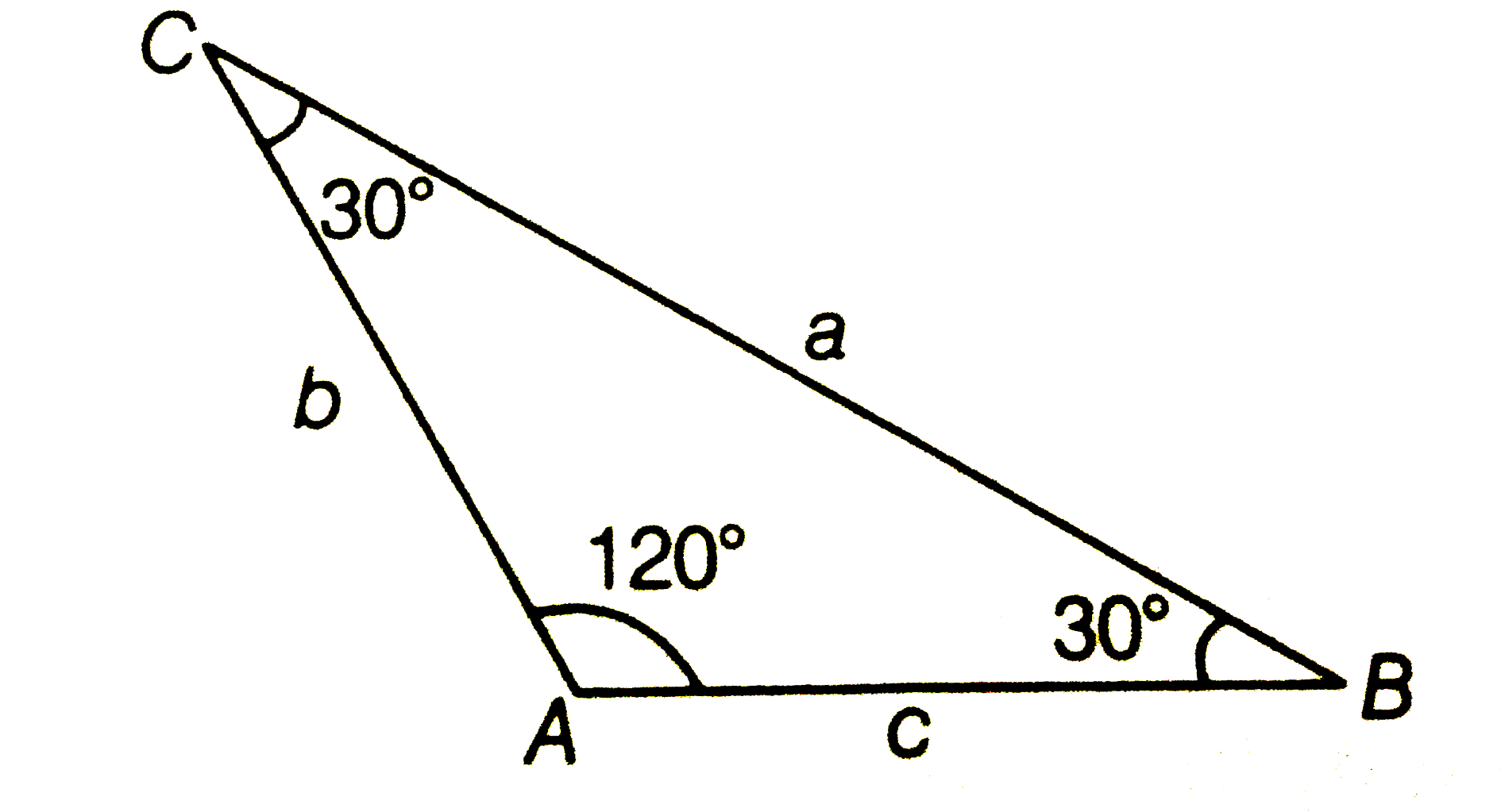
Thus ,the ratio of longest side to the perimeter `=(a)/(a+b+c)` Let b = c =x
`thereforea^(2)=b^(2)+c^(2)-2bc cosA`
`rArra^(2)=2x^(2)-2x^(2)cosA=2x^(2)(1-cosA)`
`rArra^(2)=4x^(2)"sin"^(2)(A)/(2)`
`rArra=2x"sin"(A)/(2)`
`rArra=2xsin60^(@)=sqrt(3)x`
Thus ,required ratio is
`(a)/(a+b+c)=(sqrt(3)x)/(x+x+sqrt(3)x)=(sqrt(3))/(2+sqrt(3))`