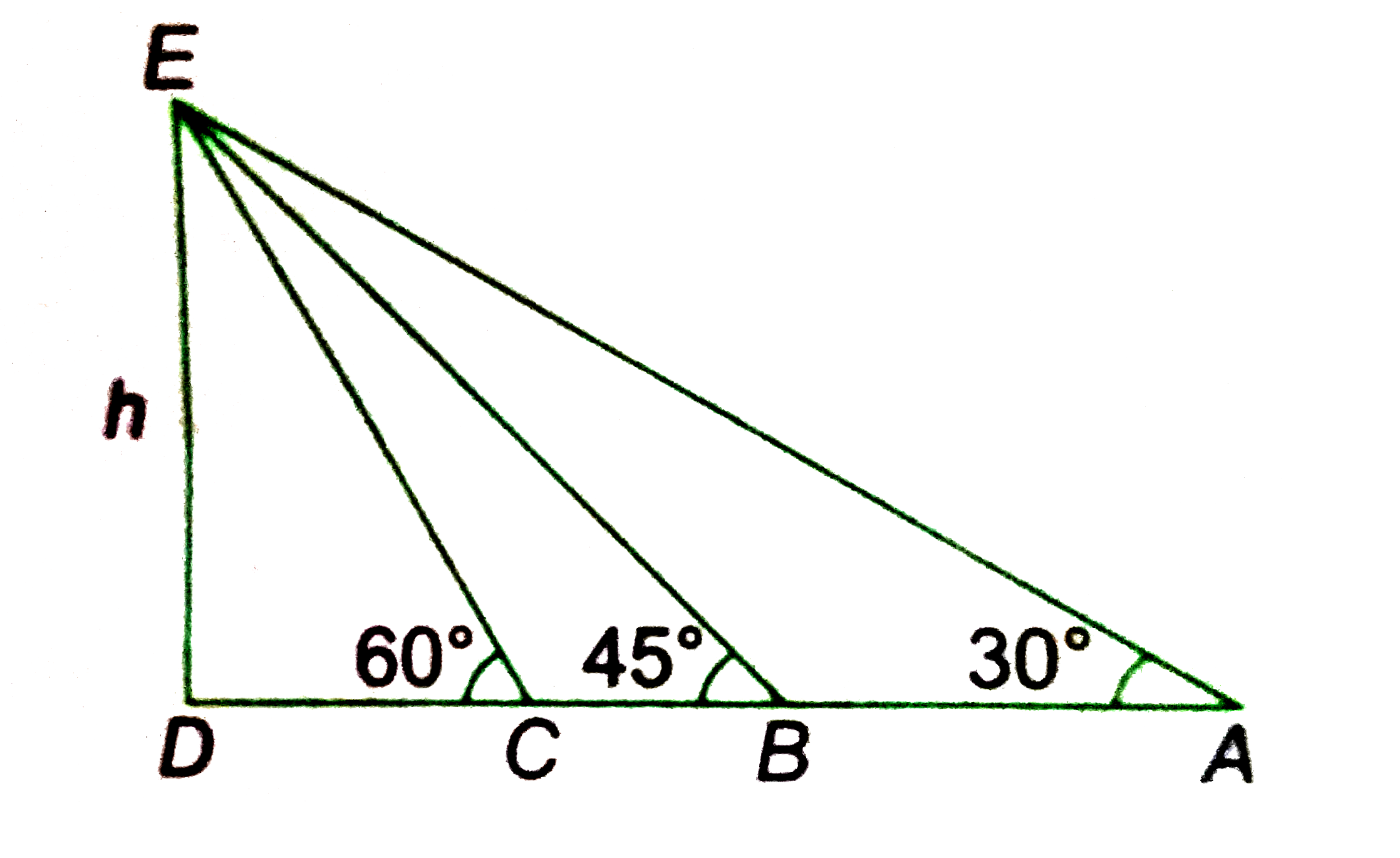
If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are $30^{0}$ , $45^{0}$ and $60^{0}$ respectively, then the ratio, AB : BC, is : (1) $\sqrt{3} : 1$ (2) $\sqrt{3} : \sqrt{2}$ (3) $1 : \sqrt{3}$ (4) $2 : 3$

A

$\sqrt{3} : 1$

B

$\sqrt{3} : \sqrt{2}$

C

$1 : \sqrt{3}$

D

$2 : 3$

Video Solution

Text Solution

Verified by Experts

Let ED be the tower of height h.
${tan 30}^{\circ} = \frac{h}{A D}$
$\Rightarrow A D = h \sqrt{3}$
$B D = h, C D = \frac{h}{\sqrt{3}}$
$\frac{A B}{B C} = \frac{A D - B D}{B D - C D}$
$\frac{h \sqrt{3} - h}{h - \frac{h}{\sqrt{3}}} = \frac{\sqrt{3} - 1}{(\frac{\sqrt{3} - 1}{\sqrt{3}})} = \sqrt{3}$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the angles of elevation of the top of tower from three collinear points $A$ , $B$ and $C$ , on a line leading to the foot of the tower, are $30^{\circ}$ , $45^{\circ}$ and $60^{\circ}$ respectively, then the ratio , $A B : B C$ is
A $\sqrt{3} : 1$
B $\sqrt{3} : \sqrt{2}$
C $1 : \sqrt{3}$
D $2 : 3$
Question 2 - Select One
Angles of elevation of the top of a tower from three point (collinear) A, B and C on a road leading to the food of the tower are $30^{\circ}, 45^{\circ}$ and $60^{\circ}$ respectively. The ratio of AB to BC is
A $\sqrt{3} : 1$
B $\sqrt{3} : 2$
C $1 : 2$
D $2 : \sqrt{3}$
Question 3 - Select One
The angle of elevation of the top of a TV tower from three points A,B and C in a straight line through the foot of the tower are $α, 2 α$ and $3 α$ , respectively. If $A B - α$ , then height of the tower is
A $a tan α$
B $a sin α$
C $a sin 2 α$
D $a sin 3 α$

CENGAGE-HIGHT AND DISTANCE -JEE Previous Year

Home
Ask Doubt
Profile