If the arcs of the same length in two circles subtend angles of 60∘ and 75∘ at their respective centres, find the ratio of their radii?
Video Solution
Text Solution
Let r1 and r2 be the radii of the two circles. Then,
θ1=60∘=(60×π180)c=(π3)c
and θ2=75∘=(75×π180)c=(5π12)c.
Let the length of each arcbe lcm. Then,
l=r1θ1=r2θ2.
⇒(r1×π3)=(r2=5π12)
⇒=r1r2=54.
Hence, r1:r2=5:4.
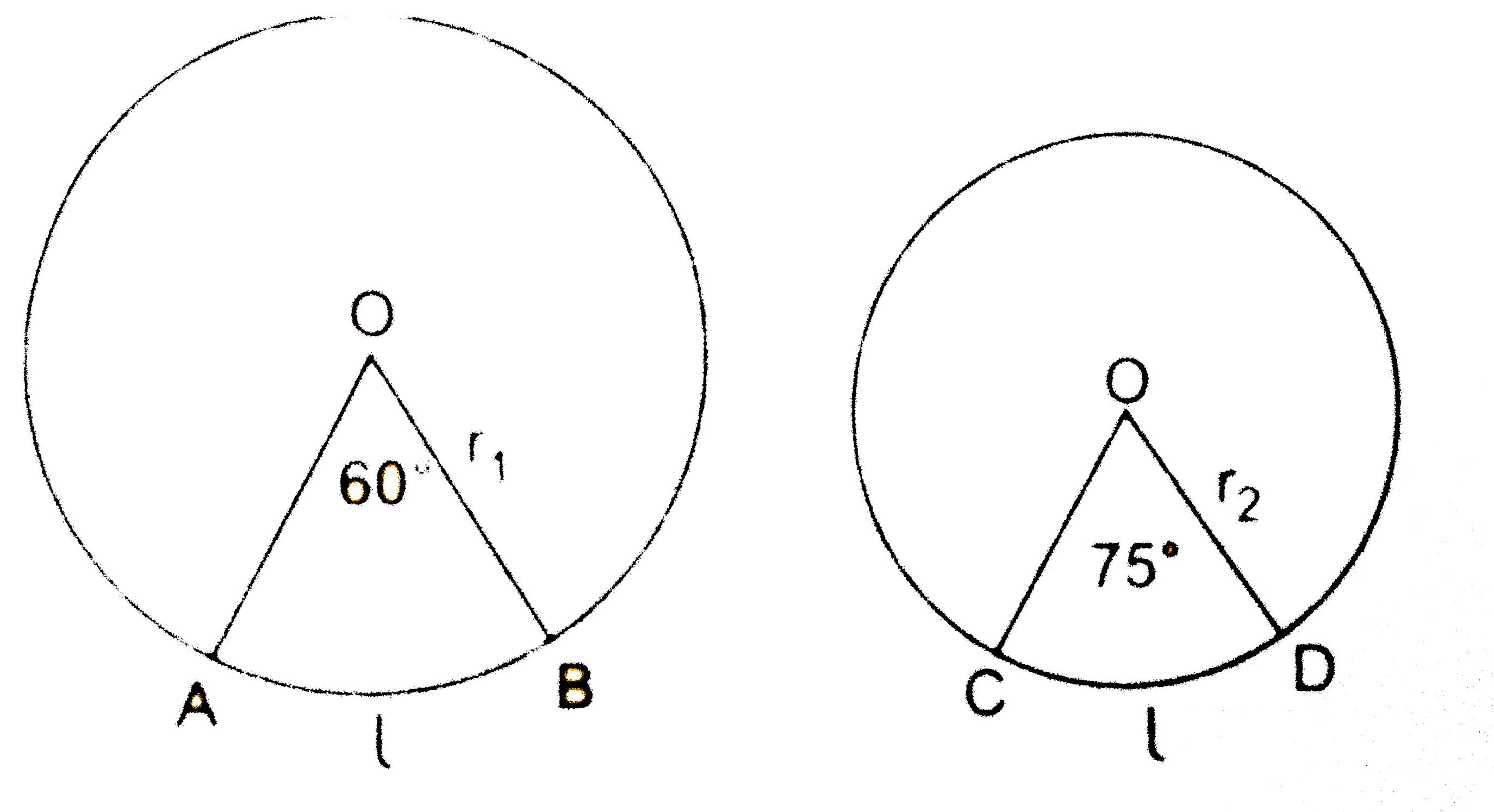 .
.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the arcs of the same length in two circles subtend angles of 60∘ and 90∘ at the centre, then the ratio of the their radii is :
A13B12C32D2If the arc of the same length in two circles subtend angles 75∘ and 120o at the centre, find the ratio of their radii.
A8:5B7:5C8:7D3:5
If the arcs of same length in two circles subtend angles of 30∘ and 45∘ at their centers, then find the ratio of their radii.
View SolutionIf arcs of same length in two circles subtend angles of 600and750 at their centers, find the ratios of their radii.
View SolutionIf the arcs of same length in two circles subtend angles of 60∘ and 75∘ at their centers. Find the ratio of their radaii.
View SolutionIf the arcs of the same length in two circle subtend angle(i)65∘ and 110∘
(ii)60∘ and 75∘ at the center,
Find the ration of their radii
View SolutionIf the arcs of the same length in two circles subtend angles 75∘ and 120∘ at the centre find the ratio of their radii
View SolutionIf the arcs of the same length in two circles subtend angles 65∘ and 110∘ at the center, then the ratio of their radii.
View Solution
