If the area enclosed between the curves y=ax2andx=ay2(a>0) is 1 square unit, then find the value of a.
A
1√3
B
12
C
1
D
13
Video Solution
Text Solution
The correct Answer is:A
We have,
1/a∫0(y2−y1)dx=1
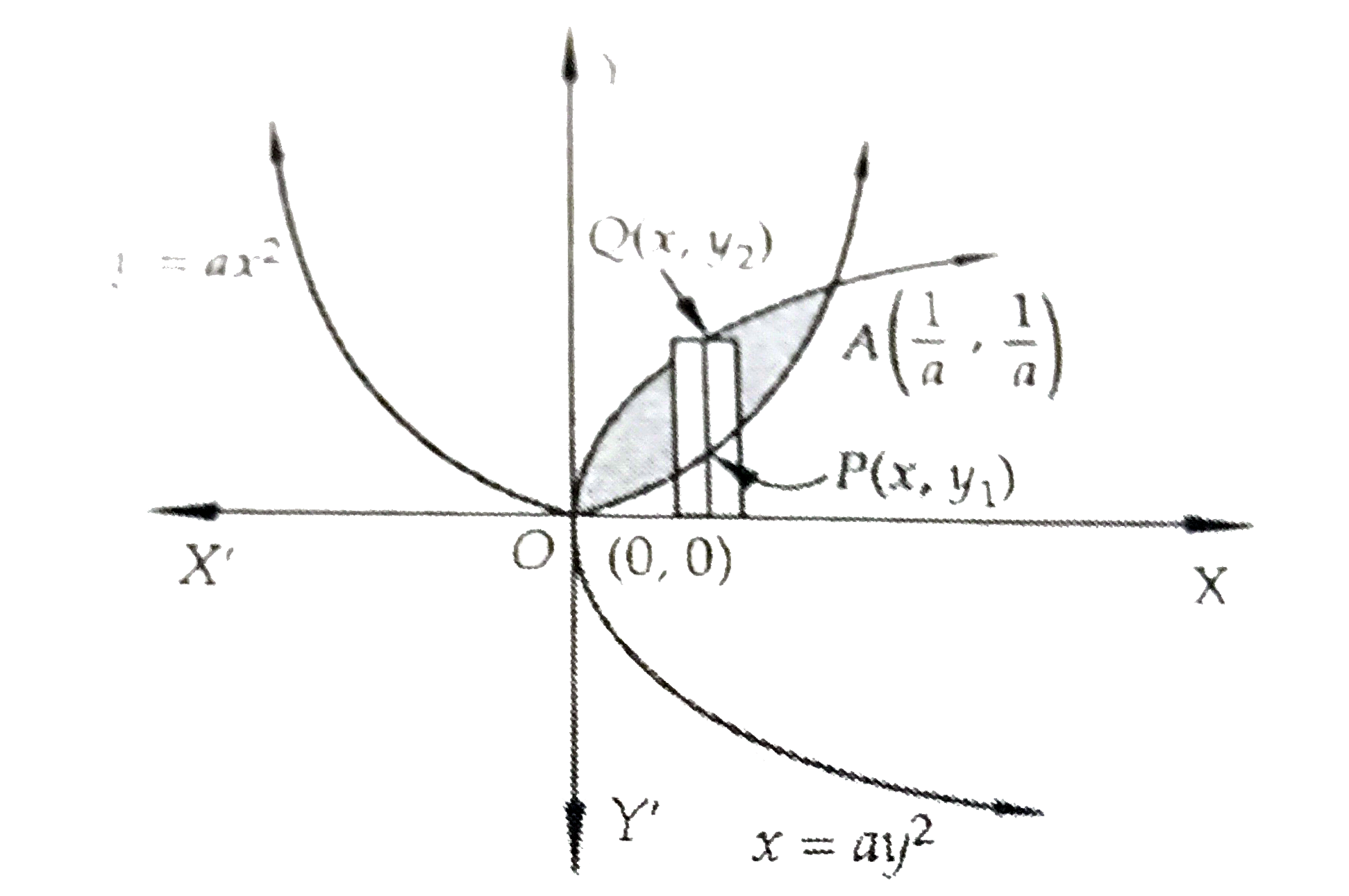
⇒1/a∫0{√xa−ax2}dx=1
⇒[23√aλ3/2−a3x3]1/a0=1⇒23√a×1a3/2−q3×1a3=1
|
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
The area enclosed between the curves y=ax2 and x=ay2(a>0) is 1 sq.unit. Then a =
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View SolutionFind the area enclosed between the curves
y=4x2 and y=x2+3
View SolutionFind the area enclosed between the curves
y=x2,y=2x−x2
View SolutionFind the area enclosed between the curves
y2=2x,y=4x−1
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed between the curves
y2=2x+6 and y=x−1
View SolutionFind the area between the curves y=xand y=x2.
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionShow that the area enclosed between the curves y = x and y=x3 is 12 sq unit.
View Solution
