If the area of the ellipse is , then find the maximum area of rectangle inscribed in the ellipse.
Video Solution
Text Solution
The correct Answer is:8 sq. units
The area of ellipse (given) . Therefore, ab=4
on the ellipse.
Now, the area of reactangle ABCD inscribed in the ellipse is
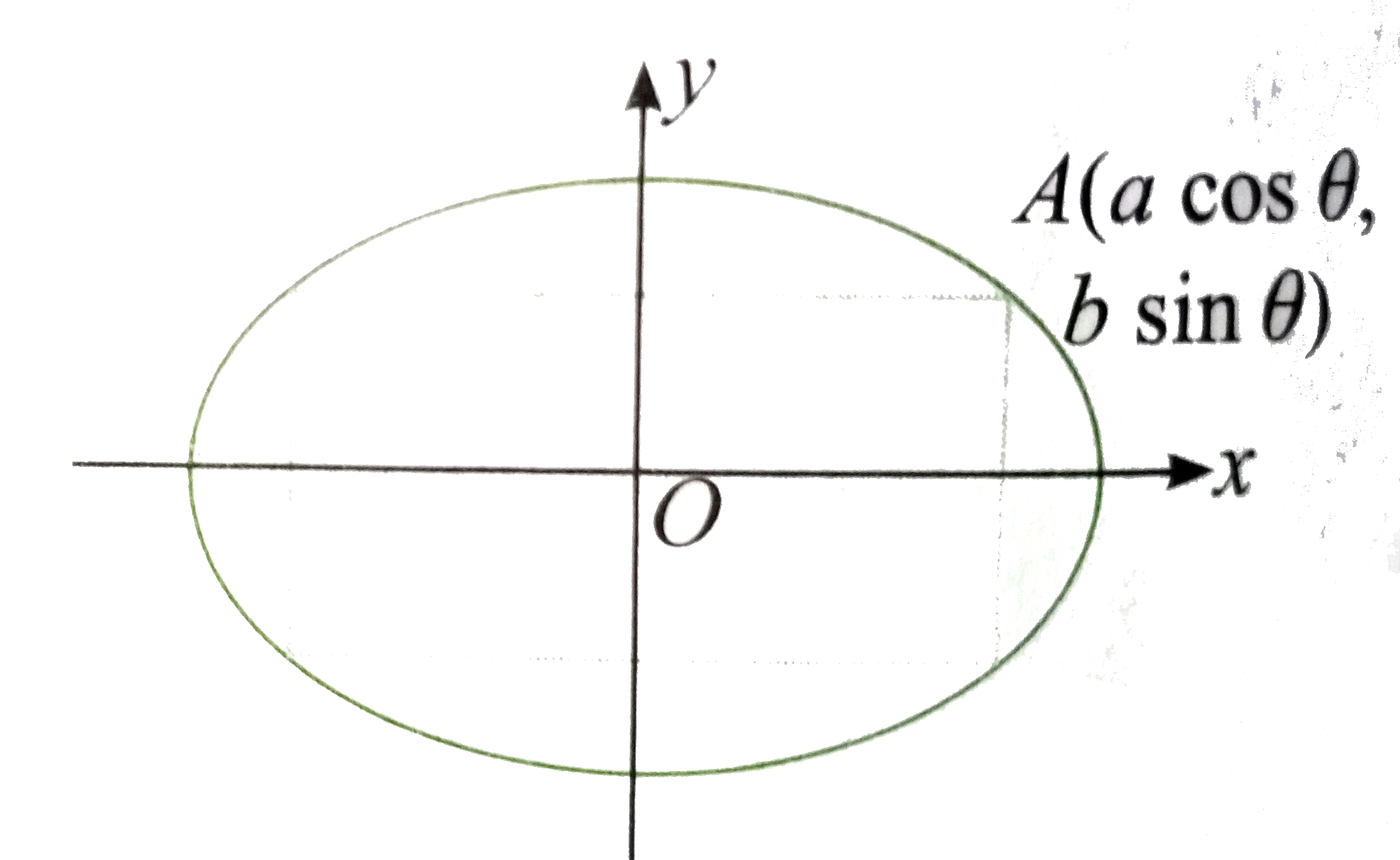
or
|
Similar Questions
Knowledge Check
What is the area of the ellipse 4x2+9y2=1.
A6πBπ36C2(e−1)De−1The area bounded by the ellipse x24+y225=1 is
A2πsq.unitsB5πsq.unitsC20πsq.unitsD10πsq.unitsConsider an ellipse x2a2+y2b2=1
What is the area of the greatest rectangle that can be inscribed in the ellipse?AabB2abCab/2D√ab
Find the area enclosed by the ellipse x2a2+y2b2=1.
View SolutionFind the area of ellipse x21+y24=1.
View SolutionFind area of the ellipsex252+y242=1.
View SolutionFind the area of the ellipse x264+y236=1.
View SolutionFind the maximum area of the ellipse x2a2+y2b2=1 which touches the line y=3x+2.
View Solution
