If the chord joining points P(α)andQ(β) on the ellipse (x2a2)+(y2b2)=1 subtends a right angle at the vertex A(a,0), then prove that tan(a2)tan(β2)=−b2a2.Solution in Bengali
mPA×mQA=−1
orbsinαacosα−a×bsinβacosβ−a=1
or4sin.α2cos.α2sin.β2cos.β2(2sin2.α2)(2sin2.β2)=−a2b2
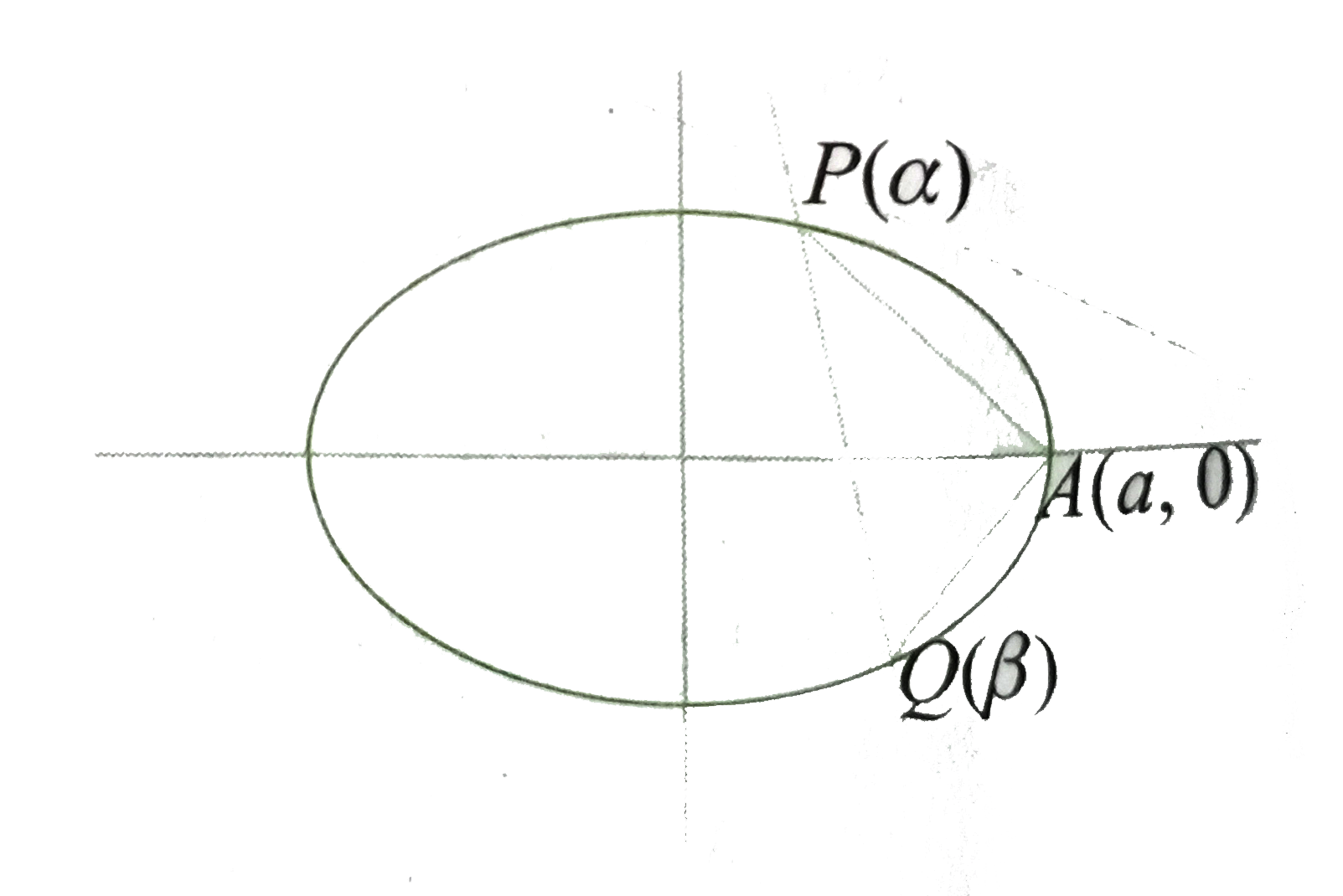
or tan.α2tan.β2=−b2a2
Similar Questions
If α−β is constant prove that the chord joining the points α and β on the ellipse x2a2+y2b2 =1 touches a fixed ellipse
10:01View SolutionProve that the chord joining points P(α) and Q(β) on the ellipse subtends a right angle at the vertex A(a,0) then tan(α2)tan(β2)=−b2a2
10:20View SolutionIf the chord joining points P(α)andQ(β) on the ellipse (x2a2)+(y2b2)=1 subtends a right angle at the vertex A(a,0), then prove that tan(a2)tan(β2)=−b2a2.
04:25View SolutionFind the equation of the chord joining point P(α)andQ(β) on the ellipse x2a2+y2b2=1.
06:40View Solutionयदि tanα=p/q जहाँ α=6β तथा α एक न्यून कोण हो, तो सिद्ध कीजिए कि : 12(p cosec 2β−qsec2β)=√p2+q2.
05:32View SolutionIf alph and beta Ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 Are the focal angles at the tip of the focal chord, then "tan"(alpha)/(2)"tan"(beta)/(2) will be honoured
03:20View SolutionProve that the chord joining points P(α)andQ(β) on the ellipse x2a2+y2b2=1 subtends a right angle at the vertex A(a,0) then tanα2tanβ2=−b2a2.
View Solutionयदि दीर्घवृत्त x2a2+y2b2=1 की एक नाभीय जीवा के सिरों के उत्केन्द्र कोण α एवं β है, तो tanα/2tanβ/2 बराबर है
05:21View Solution

