If the coordinates of the middle point of the portion of a line interceptecd between the coordinate axes is (3,2), then the equation of the line will be
2x+3y=12
3x+2y=12
4x−3y=6
5x−2y=10
The correct Answer is:A
Since, the coordinate of the middle point are P (3,2)
∴3=1.0+1.a1+1
⇒3=a2⇒a=6
Similarly, b=4
∴ Equation of the line is x6+y4=1
⇒2x+3y=12
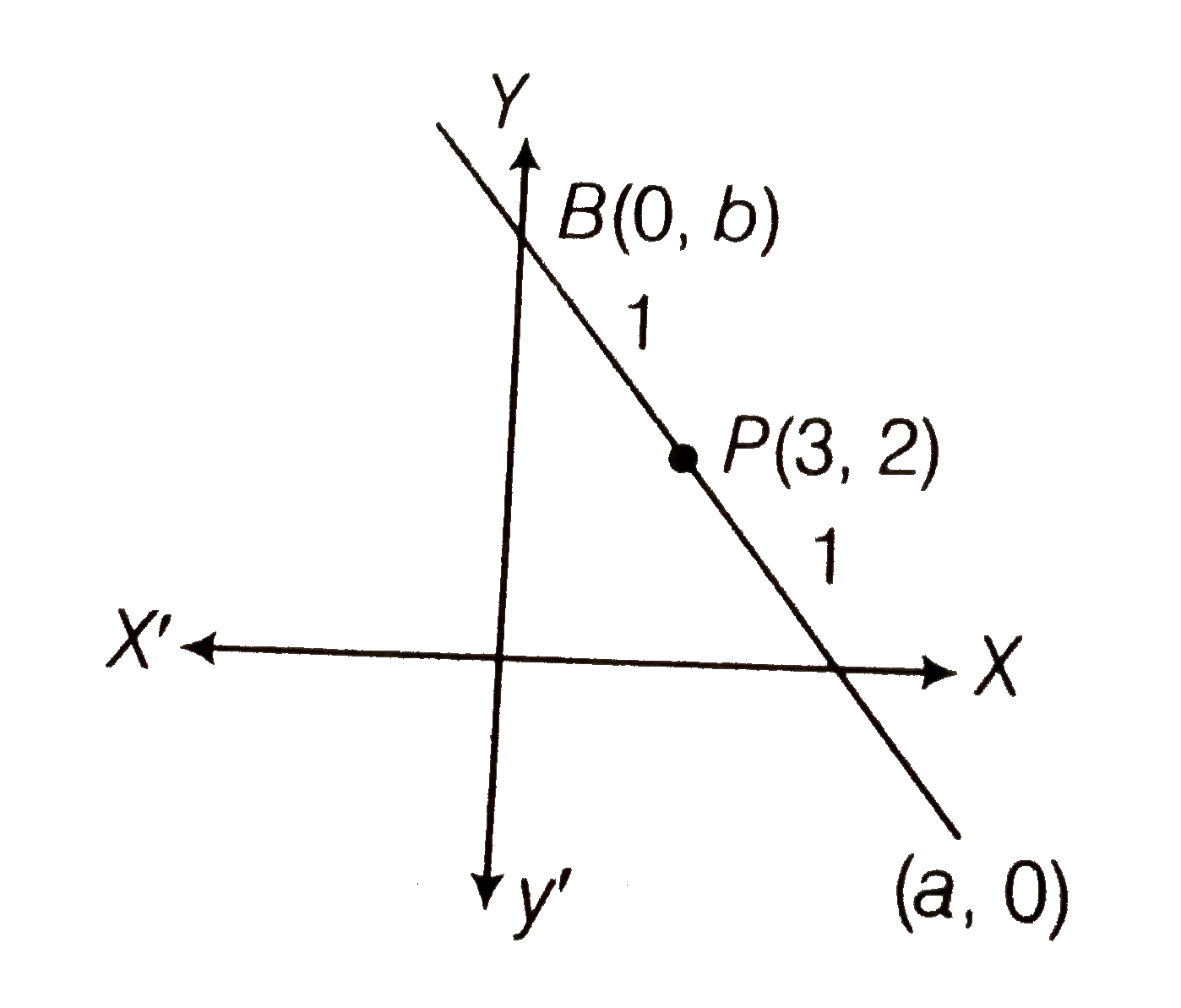
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Fillers
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - TRUE/FALSE
9 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Long Answer type
9 Videos
- STATISTICSBOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
Similar Questions
Knowledge Check
If (2,3) is the midpoint of the portion of a line intercepted between the co-ordinate axes , then the equation of the line is
A2x+3y=12B2x+3y+12=0C3x+2y=12Dnone of theseFind the locus of mid-point of the portion of tangent intercepted between coordinate axes to the circle x2+y2=1.
Ax2+y2−4x2y2=0Bx2+y2−2xy=0Cx2+y2−2x2Y2=0Dx2y2=0The projection of a line segment on the coordinate axes are 2,3,6. Then the length of the line segment is
A7B5C1D11
A line passes through (−3,4) and the portion of the line intercepted between the coordinate axes is bisected at the point then equation of line is (A) 4x−3y+24=0 (B) x−y−7=0 (C) 3x−4y+25=0 (D) 3x−4y+24=0
View SolutionA straight line passes through the point (α,β) and this point bisects the portion of the line intercepted between the axes. Show that the equation of the straight line is x2α+y2β=1.
View SolutionFind the equation of the line whose portion intercepted between the coordinate axes is divided at the point (5, 6) in the ratio 3:1.
View SolutionThe equation of the line which is such that the portion of line segment intercepted between the coordinate axes is bisected at (4,-3) ,is
View SolutionIf the portion of a line intercepted between the coordinate axes is divided by the point (2,−10 in the ratio 3:2. then the equation of that line is
View Solution
