If the cost and revenue funcation of a product are respectively C(x)=5x+700 and R(x)=15x+100 , where x is the number of products then what will be the value of x to get profit ?
The correct Answer is:N/a
To determine the value of x that results in a profit, we start by defining the profit in terms of the cost and revenue functions.
1. Identify the Cost and Revenue Functions:
- Cost function: C(x)=5x+700
- Revenue function: R(x)=15x+100
2. Define Profit:
- Profit occurs when revenue exceeds cost. Therefore, we need to set up the inequality:
R(x)>C(x)
3. Substitute the Functions into the Inequality:
- Substitute R(x) and C(x) into the inequality:
15x+100>5x+700
4. Rearrange the Inequality:
- To isolate x, we first subtract 5x from both sides:
15x−5x+100>700
- This simplifies to:
10x+100>700
5. Isolate the Variable:
- Next, subtract 100 from both sides:
10x>700−100
- This simplifies to:
10x>600
6. Solve for x:
- Finally, divide both sides by 10:
x>60
7. Conclusion:
- The value of x must be greater than 60 for the company to make a profit. Thus, the solution is:
x>60
- Cost function: C(x)=5x+700
- Revenue function: R(x)=15x+100
- Profit occurs when revenue exceeds cost. Therefore, we need to set up the inequality:
R(x)>C(x)
- Substitute R(x) and C(x) into the inequality:
15x+100>5x+700
- To isolate x, we first subtract 5x from both sides:
15x−5x+100>700
- This simplifies to:
10x+100>700
- Next, subtract 100 from both sides:
10x>700−100
- This simplifies to:
10x>600
- Finally, divide both sides by 10:
x>60
- The value of x must be greater than 60 for the company to make a profit. Thus, the solution is:
x>60
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - NCERT QUESTION
51 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- MATHEMATICAL REASONING BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise
7 Videos
Similar Questions
Knowledge Check
If 5x=15x+20, what is the value of x5 ?
A10B5C2D12If the demand function for a product is p=80−π4, where x is the number of units and p is the price per unit, the value of x for which the revenue will be maximum is
A40B20C10D80
A company manufactures cassettes. Its cost and revenue functions are C(x)=26000+30x and R(x)= 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit ?
View SolutionThe cost function of a product is given by C(x)=x33−45x2−900x+36 where x is the number of units produced. How many units should be produced to minimise the marginal cost ?
View SolutionA company manufactures cassettes and its cost and revenue functions for a week are C=300+32x and R=2x respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold for the company to realize a profit?
View SolutionThe major product of "X" and "Y" are respectively

View Solution2x+5y=2y−6
5x+2y=7
In the system of equations above, what is the value of the product xy?
View Solution700, 1200, 1600, 2000, x
If the mean of the five numbers above is 1600, what is the value of x ?
View Solution

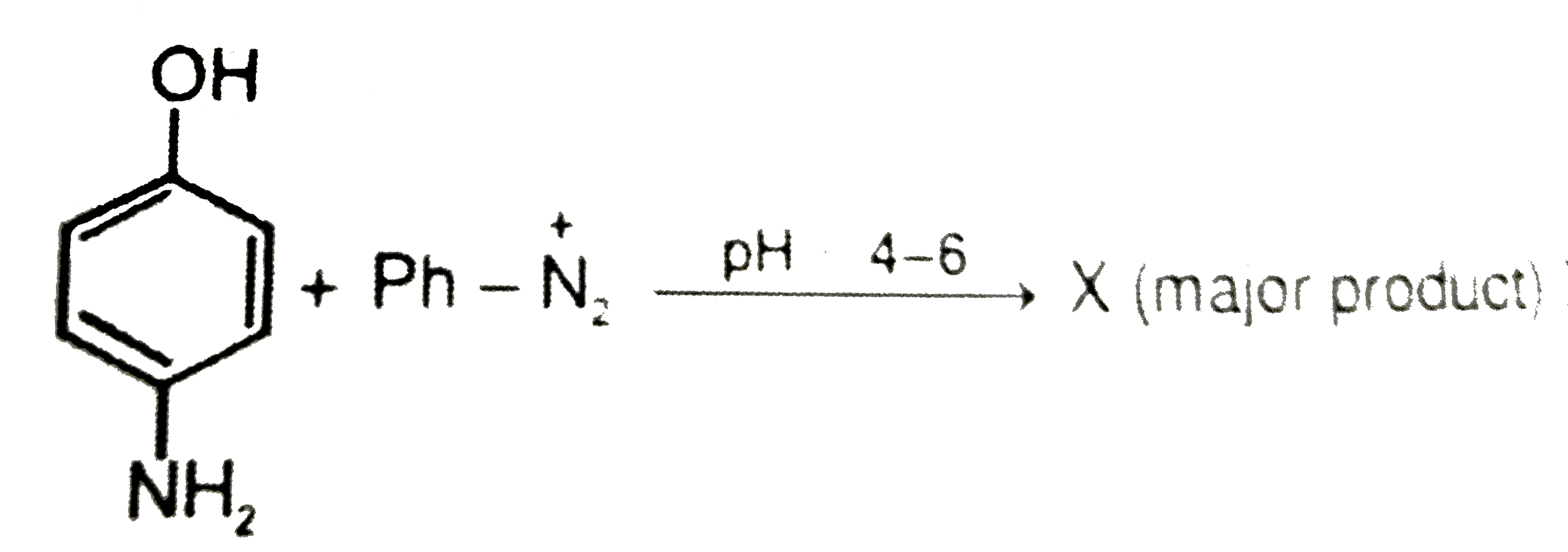 X (major product ) X will be -
X (major product ) X will be -