If the diagonals of a parallelogram ABCD are along the lines x+5y=7 and 10x−2y=9, then ABCD must be a
rectangle
square
cyclic quadrilateral
rhombus
The correct Answer is:D
To determine the type of parallelogram ABCD based on the given diagonals, we will follow these steps:
Step 1: Identify the equations of the diagonals
The diagonals of the parallelogram are given by the equations:
1. x+5y=7
2. 10x−2y=9
Step 2: Find the slopes of the lines
To find the slopes of these lines, we will rearrange them into the slope-intercept form y=mx+b, where m is the slope.
For the first line x+5y=7:
5y=−x+7y=−15x+75
Thus, the slope m1=−15.
For the second line 10x−2y=9:
−2y=−10x+9y=5x−92
Thus, the slope m2=5.
Step 3: Check if the diagonals are perpendicular
To check if the diagonals are perpendicular, we multiply the slopes m1 and m2:
m1⋅m2=(−15)⋅5=−1
Since the product of the slopes is −1, the diagonals are perpendicular.
Step 4: Determine the type of parallelogram
In a parallelogram, if the diagonals are perpendicular, it indicates that the parallelogram is a rhombus. Therefore, the type of parallelogram ABCD must be a rhombus.
Final Answer
ABCD must be a rhombus.
---
The diagonals of the parallelogram are given by the equations:
1. x+5y=7
2. 10x−2y=9
To find the slopes of these lines, we will rearrange them into the slope-intercept form y=mx+b, where m is the slope.
5y=−x+7y=−15x+75
Thus, the slope m1=−15.
−2y=−10x+9y=5x−92
Thus, the slope m2=5.
To check if the diagonals are perpendicular, we multiply the slopes m1 and m2:
m1⋅m2=(−15)⋅5=−1
Since the product of the slopes is −1, the diagonals are perpendicular.
In a parallelogram, if the diagonals are perpendicular, it indicates that the parallelogram is a rhombus. Therefore, the type of parallelogram ABCD must be a rhombus.
ABCD must be a rhombus.
Topper's Solved these Questions
Similar Questions
The diagonals of a parallelogram PQRS are along the lines x+3y =4 and 6x-2y = 7, Then PQRS must be :
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
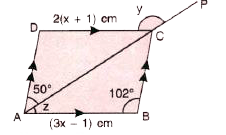
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
View SolutionProve that the diagonals of the parallelogram formed by the four lines 3x+y=0,3y+x=0,3x+y=4,3y+x=4 are at right angles.
View SolutionTwo sides of a parallelogram are along the lines x+y=3 and x=y+3. If its diagonals intersect at (2, 4) , then one of its vertices is
View SolutionProve that the diagonals of the parallelogram formed by the lines √3x+y=0,√3y+x=0,√3x+y=1and√3y+x=1 are at right angles.
View SolutionThe diagonal of the rectangle formed by the lines x2−7x+6=0 and y2−14y+40=0 is
View SolutionIf one of the diagonals of a square is along the line x=2y and one of its vertices is (3, 0), then its sides through this vertex are given by the equations (A) y−3x+9=0,3y+x−3=0 (B) y+3x+9=0,3y+x−3=0 (C) y−3x+9=0,3y−x+3=0 (D) y−3x+9=0,3y+x+9=0
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BY. Prove that □AXCY is a parallelogram.
View SolutionThe sides AB and AD of a parallelogram ABCD are 2x−y+1=0andx+3y−10=0 respectively and C is the point (−1,−2). Find the equation of the diagonals AC.
View Solution
