If the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
The correct Answer is:5.72m
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry of the Problem
We have a parabolic rope suspended between two towers. The height of the towers is 20 m, the distance between the towers is 150 m, and the lowest point of the rope is 3 m above the road.
Step 2: Set Up the Coordinate System
Let's set the origin (0, 0) at the lowest point of the rope. Therefore, the coordinates of the towers will be:
- Left tower: (-75, 20) (since the distance from the center is half of 150 m)
- Right tower: (75, 20)
Step 3: Determine the Vertex of the Parabola
The vertex of the parabola (the lowest point of the rope) is at (0, 3).
Step 4: Use the Standard Form of the Parabola
The equation of a parabola that opens upwards can be written as:
y=ax2+bx+c
Since the vertex is at (0, 3), we can rewrite the equation as:
y=a(x2)+3
Step 5: Use the Coordinates of the Towers to Find 'a'
We know that the height of the towers is 20 m, so we can use the coordinates of one of the towers to find 'a'. Let's use the left tower (-75, 20):
20=a(−75)2+3
20=5625a+3
5625a=20−3
5625a=17
a=175625
Step 6: Write the Equation of the Parabola
Substituting 'a' back into the equation:
y=175625x2+3
Step 7: Find the Height of the Tower at 30 m from the Center
To find the height of the tower that is 30 m from the center, we substitute x=30 into the equation of the parabola:
y=175625(302)+3
y=175625(900)+3
y=153005625+3
y=2.72+3
y=5.72
Step 8: Calculate the Height of the Tower
The height of the tower at a distance of 30 m from the center is:
Height=5.72 m
Final Answer
The equation of the parabolic shape of the rope is:
y=175625x2+3
The height of the tower at a distance of 30 m from the center is 5.72 m.
---
We have a parabolic rope suspended between two towers. The height of the towers is 20 m, the distance between the towers is 150 m, and the lowest point of the rope is 3 m above the road.
Let's set the origin (0, 0) at the lowest point of the rope. Therefore, the coordinates of the towers will be:
- Left tower: (-75, 20) (since the distance from the center is half of 150 m)
- Right tower: (75, 20)
The vertex of the parabola (the lowest point of the rope) is at (0, 3).
The equation of a parabola that opens upwards can be written as:
y=ax2+bx+c
Since the vertex is at (0, 3), we can rewrite the equation as:
y=a(x2)+3
We know that the height of the towers is 20 m, so we can use the coordinates of one of the towers to find 'a'. Let's use the left tower (-75, 20):
20=a(−75)2+3
20=5625a+3
5625a=20−3
5625a=17
a=175625
Substituting 'a' back into the equation:
y=175625x2+3
To find the height of the tower that is 30 m from the center, we substitute x=30 into the equation of the parabola:
y=175625(302)+3
y=175625(900)+3
y=153005625+3
y=2.72+3
y=5.72
The height of the tower at a distance of 30 m from the center is:
Height=5.72 m
The equation of the parabolic shape of the rope is:
y=175625x2+3
The height of the tower at a distance of 30 m from the center is 5.72 m.
Topper's Solved these Questions
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - JEE type solved examples
1 Videos
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise For Session 1
20 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
28 Videos
Similar Questions
The height of a tower is 200 m. A model of this tower is made such that the ratio between the height of the actual tower and that of the model is 160:1. Find the height of the model.
View SolutionThe height of a tower is 132m. A model of this tower is made such that the ratio between the height of the actual tower and that of the model is 120:1. Find the height of the model.
View Solution
Knowledge Check
The angle of elevation of the top of a tower. from a point on the ground and at a distance of 160 m from its foot, is find to be 60∘ . Find the height of the tower .
A277.12 mB377.12 mC477.12 mDNone
The distance between two towers is 140 m while seeing from the top if the second tower, the angle of elevation of first tower is 30∘.If the height of the second tower is 60 m, then find the height of the first tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
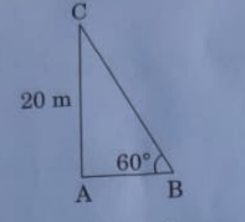
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.

View SolutionIn figure the tension in the rope (rope is light) is

View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of depression of a car parked on the road from the top of the 150 m high tower is 30∘.Find the distance of the car from the tower
View Solution
