If the eccentric angles of two points P and Q on the ellipse x228+y27=1 whose centre is C differ by a right angle then the area of ΔCPQ isSolution in Bengali
5
6
7
8
The correct Answer is:C
If P is the point (acosθ,bsinθ), the coordinates of Q are (acos(θ+π2),bsin(θ+π2))
i.e., (−asinθ,bcosθ) where a2=28,b2=7
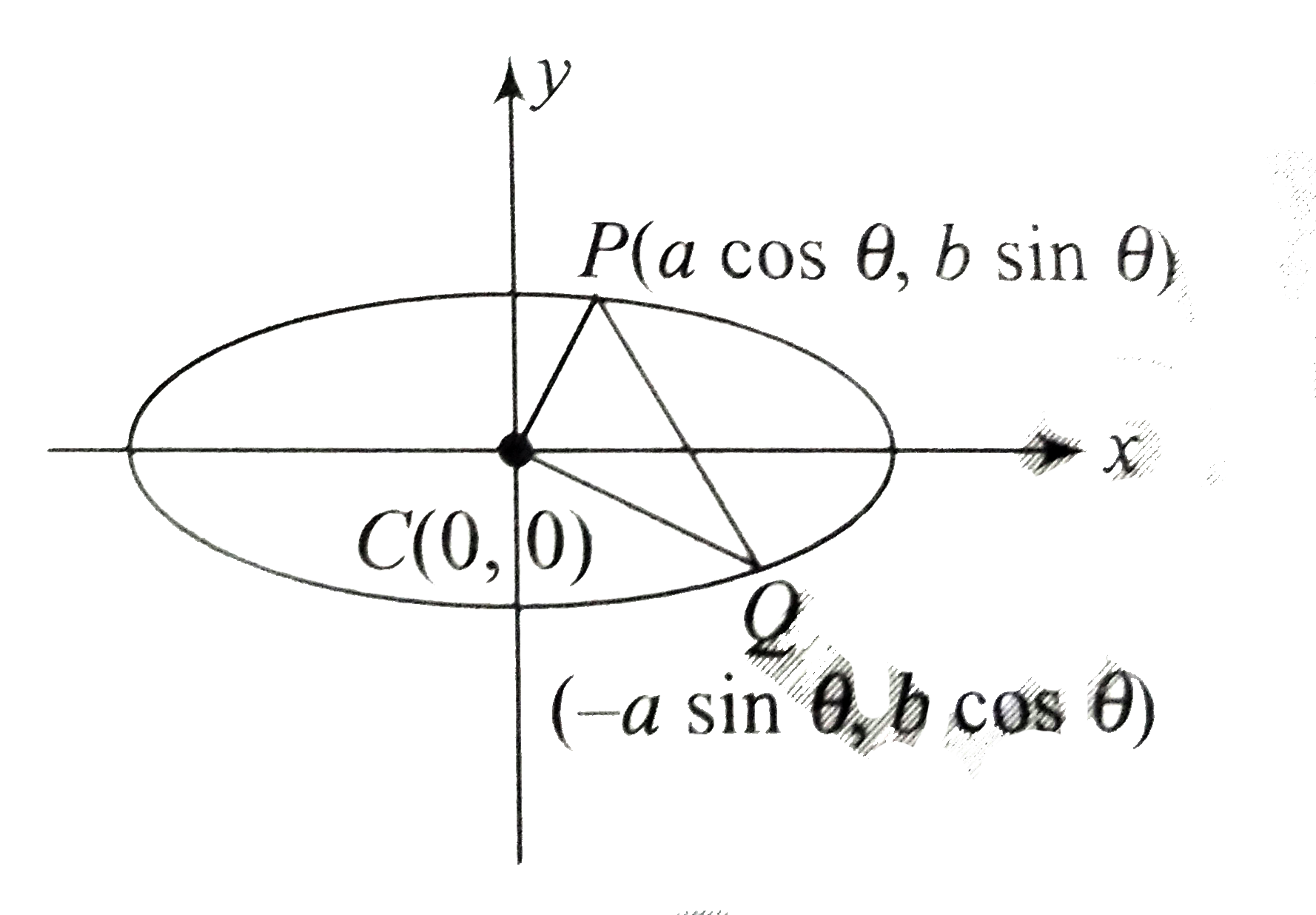
∴ The area of ΔCPQ=12∣∣abcos2θ+absin2θ∣∣{∵area=∣∣∣{12(x1y2−x2y2)}∣∣∣}
=12ab
=12(√28)(√7)=7 sq units.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - ELLIPSE EXERCISE - Multiple Correct Answers Type6videos
ELLIPSE
- BOOK - CENGAGE PUBLICATIONCHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
- BOOK - CENGAGE PUBLICATIONCHAPTER - EQAUTION OF STRAIGHT LINE AND ITS APPLICATION EXERCISE - DPP 3.213videos
EQAUTION OF STRAIGHT LINE AND ITS APPLICATION
Similar Questions
In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
08:02View SolutionLet a,bgt0 and α=ˆia+4ˆjb+bˆk and β=bˆi+aˆtj+1bˆk, then the maximum value of 105+α⋅β is
08:16View SolutionThe ratio in which the plane 2x−1=0 divides the line joining (−2,4,7) and (3,−5,8) is
09:46View SolutionArea of the triangle formed by the tangents at the point on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 whose eccentric angles are alpha,beta,gamma is
03:18View SolutionThe area of the triangle formed by three points on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 whose eccentric angles are alpha,beta and gamma is
11:46View SolutionP and Q are points on the ellipse x^2/a^2+y^2/b^2 =1 whose center is C. The eccentric angles of P and Q differ by a right angle. If /_PCQ minimum, the eccentric angle of P can be (A) pi/6 (B) pi/4 (C) pi/3 (D) pi/12
02:29View SolutionIf the eccentric angles of two points P and Q on the ellipse (x^(2))/(28)+(y^(2))/(7)=1 whose centre is C differ by a right angle then the area of Delta CPQ is
03:13View SolutionP and Q are two points on the ellipse x2a2+y2b2=1 whose eccentric angles are differ by 90∘, then
02:20View SolutionThe eccentric angle of a point on the ellipse x26+y22=1 whose distance from the centre of the ellipse is 2, is
02:53View SolutionThe points on the ellipse 2x2+3y2=6 whose eccentric angles differ by two right angles is
03:00View SolutionThe points on the ellipse x225+y29=1 Whose eccentric angles differ by a right angle are
14:53View SolutionIf the eccentric angles of two points P and Q on the ellipse x228+y27=1 whose centre is C differ by a right angle then the area of ΔCPQ is
02:27View SolutionPandQ are points on the ellipse x2a2+y2b2=1 whose center is C. The eccentric angles of P and Q differ by a right angle. If ∠PCQ minimum, the eccentric angle of P can be (A) π6 (B) π4 (C) π3 (D) π12
03:16View SolutionP and Q are two points on the ellipse x2a2+y2b2=1 whose eccentric angles are differ by 90∘, then
04:49View SolutionThe eccentric angle of a point on the ellipse x26+y22=1 whose distance from the centre of the ellipse is 2, is
03:12View SolutionArea of the triangle formed by the tangents at the point on the ellipse x2a2+y2b2=1 whose eccentric angles are α,β,γ is
05:30View Solution

