If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then the value of c is aa2−a22+b12−b22 √a12+b12−a22−b22 12(a12+a22+b12+b22) 12(a22+b22−a12−b12)Solution in Punjabi
a21−a22+b21−b22
√(a21+b21−a22−b22)
12(a21+a22+b21+b22)
12(a22+b22−a21−b21)
The correct Answer is:D
Step by step video solution for If the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise For Session 6
12 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Single Option Correct Type Questions)
28 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise For Session 4
15 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
Similar Questions
A ray of light passes through the point (1, 2) reflects on the x-axis at a point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
View SolutionThe straight line y=x−2 rotates about a point where it cuts the x-axis and becomes perpendicular to the straight line ax+by+c=0. Then its equation is
View SolutionThree straight lines 2x+11y−5=0,24x+7y−20=0and4x−3y−2=0
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View SolutionIn the quadratic equation ax2+bx+c=0. if δ=b2−4ac and α+β,α2+β2,α3+β3 are in G.P. and α,β are the roots of ax2+bx+c=0
View SolutionLet →a=a1ˆi+a2ˆj+a2ˆk,→b=b1ˆi+a2ˆj+b2ˆk,and→c=c1ˆi+c2ˆj+c2ˆk, be three non-zero vectors such that →c is a unit vector perpendicular to both vectors →aand→b . If the angle between aandb is π/6, then |a1a2a3b1b2b3c1c2c3|2 is equal to 0 1 14(a12+a22+a32)(b12+b22+b32) 34(a12+a22+a32)(b12+b22+b32)(c12+c22+c32)
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆkand→c=c1ˆi+c2ˆj+c3ˆk be three nonzero vectors such that →c is a unit vector perpendicular to both →aand→b. If the angle between →aand→b is π/6 , then the value of |a1b1c1a2b2c2a3b3c3| is a.0 b. 1 c. 14(a12+a22+a32)(b12+b22+b32) d. 34(a12+a22+a32)(b12+b22+b32)
View SolutionLet a1,a2,a3 ...... a11 be real numbers satisfying a_1 =15, 27-2a_2 > 0 and a_k= 2a_(k-1) - a_(k-2) for k=3,4,.....11 If (a1^2 +a2^2.......a11^2)/11 = 90 then find the value of (a_1+a_2....+a_11)/11
View Solution(x2a21)+(y2b21)=1 ((a21)>(b21)) এবং(x2a22)+(y2b22)=1((a22)>(b22)) উপবৃত্তদ্বয়ের উৎকেন্দ্ৰতা সমান হলে, দেখাও যে a1b2,=a2b1 |
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
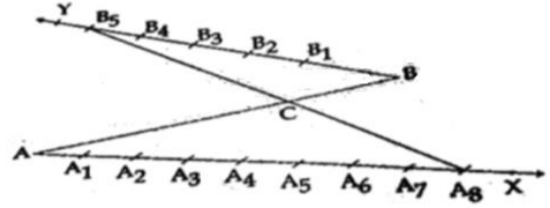
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionLet a1,a2,a3,,a11 be real numbers satisfying a1=15,27−2a2>0andak=2ak−1−ak−2 for k=3,4,,11. If a12+a22+...+a11211=90, then the value of a1+a2++a1111 is equals to _______.
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆkand→c=c1ˆi+c2ˆj+c3ˆk be three nonzero vectors such that →c is a unit vector perpendicular to both →aand→b. If the angle between →aand→b is π/6 , then the value of |a1b1c1a2b2c2a3b3c3|2 is a.0 b. 1 c. 14(a12+a22+a32)(b12+b22+b32) d. 34(a12+a22+a32)(b12+b22+b32)
View SolutionLet a1,a2,a3 ...... a11 be real numbers satisfying a1=15,27−2a2>0andak=2ak−1−ak−2 for k=3,4,.....11 If a12+a22.......a11211=90 then find the value of a1+a2....+a1111
View Solution
