If the equation $∣ ∣ x^{2} - 5 x + 6 ∣ ∣ - λ x + 7 λ = 0$ has exactly 3 distinct solutions then $λ$ is equal to

A

$- 7 + \sqrt{23}$

B

$- 9 + 4 \sqrt{5}$

C

$- 7 - \sqrt{23}$

D

$- 9 - 4 \sqrt{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$(b)$ $∣ ∣ x^{2} - 5 x + 6 ∣ ∣ - λ x + 7 λ = 0$ has exactly three solutions,
$∴$ as shown in the graph
$- x^{2} + 5 x - 6 = λ x - 7 λ$ must have equal roots

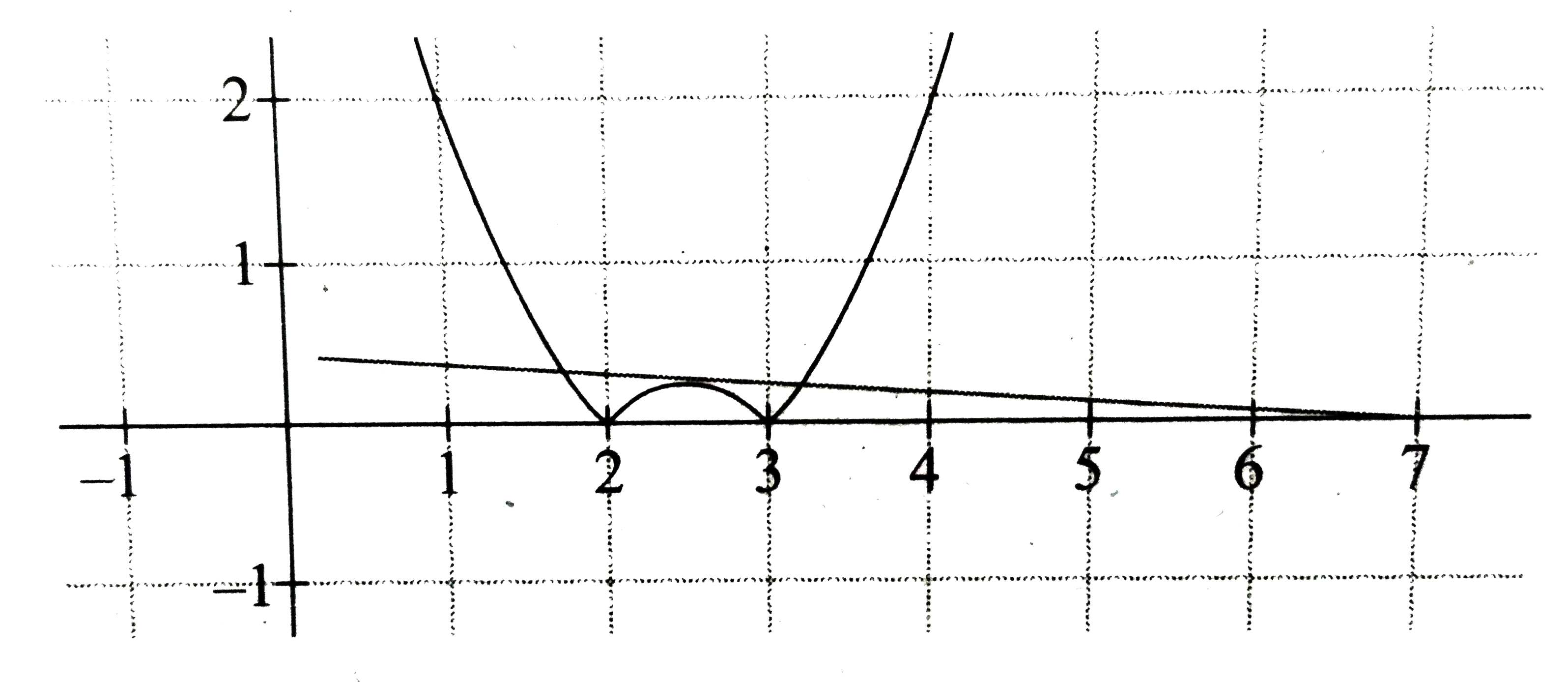
$∴ x^{2} + (λ - 5) x + 6 - 7 λ = 0$ has discriminant zero
$\Rightarrow λ = - 9 + 4 \sqrt{5}$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the equation $x^{3} - 6 x^{2} + 9 x + λ = 0$ has exactly one root in (1, 3), then $λ$ belongs to the interval
A $(- 6, - 3)$
B $(- 4, 0)$
C $(- 2, 2)$
D $(- 1, 3)$
Question 2 - Select One
Let $λ$ be a real number for which the system of linear equations
$x + y + z = 6$
$4 x + λ y - λ z = λ - 2$
$3 x + 2 y - 4 z = - 5$
has infinity many solutions then $λ$ is a root of the quadratic equation:
A $λ^{2} + 3 λ - 4 = 0$
B $λ^{2} - 3 λ - 4 = 0$
C $λ^{2} + λ - 6 = 0$
D $λ^{2} - λ - 6 = 0$

CENGAGE-THEORY OF EQUATIONS-JEE Advanced Previous Year

Home
Ask Doubt
Profile