If the equation ∣∣x2−5x+6∣∣−λx+7λ=0 has exactly 3 distinct solutions then λ is equal to Solution in Bengali
−7+√23
−9+4√5
−7−√23
−9−4√5
The correct Answer is:B
(b) ∣∣x2−5x+6∣∣−λx+7λ=0 has exactly three solutions,
∴ as shown in the graph
−x2+5x−6=λx−7λ must have equal roots
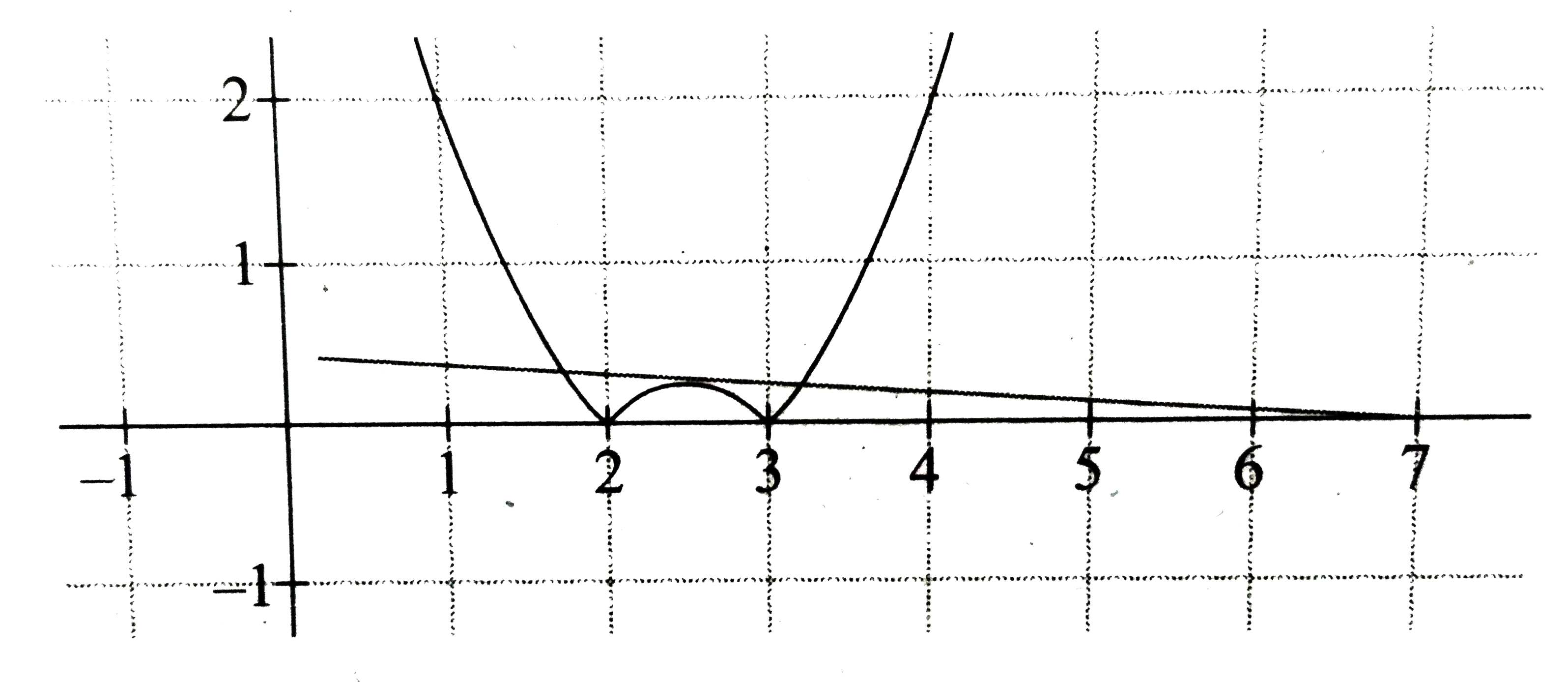
∴x2+(λ−5)x+6−7λ=0 has discriminant zero
⇒λ=−9+4√5
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - ILLUSTRATION
121 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
Similar Questions
If c≠0 and the equation p/(2x)=a/(x+c)+b/(x−c) has two equal roots, then p can be a. (√a−√b)2 b. (√a+√b)2 c. a+b d. a−b
View Solutionf(x) be a quadratic polynomial f(x)=(x−1)(ax+b) satisfying f(2)+f(4)=0.
If unity is one root of f(x) = 0 then find the other root.
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe system of linear equations x+λy−z=0 λx−y−z=0 x+y−λz=0 has a non-trivial solution for : (1) infinitely many values of λ . (2) exactly one value of λ . (3) exactly two values of λ . (4) exactly three values of λ .
View SolutionIf the equation x2+2(λ+1)x+λ2+λ+7=0 has only negative roots, then the least value of λ equals__________.
View SolutionThe number of integral values of λ for which exactly one root of the equation 5x2+(λ+1)x+λ=0 lies in the interval (1,3) is
View SolutionIf the equation |x^(2)-5x+6|-lambda x+7 lambda=0 has exactly 3 distinct solutions then lambda is equal to
View SolutionEquation |x-3|-|x-5|=lambda has exactly one real solution if lambda is equal to
View SolutionEquation |x-3|-|x-5|=lambda has exactly one real solution if lambda is equal to
View SolutionThe number of solutions of the equation x3+2x2+5x+2cosx=0 in [0,2π] is λ then λ4=
View SolutionThe sum of distinct value of λ for which the system of equations
(λ−1)x+(3λ+1)y+2λx=0
(λ−1)x+(4λ−2)y+(λ+3)x=0
2x+(2λ+1)y+3(λ−1)z=0
has non - zeor solutions is ______.
View SolutionA solutions set of the equations x+2y+z=1,x+3y+4z=k,x+5y+10z=k2
(5λ−1,1−3λ,λ)
(1+5λ,−3λ,λ)
(1+6λ,−2λ,λ)
(1−6λ,λ,λ)
View SolutionIf the equation x2+2(λ+1)x+λ2+λ+7=0 has only negative roots, then the least value of λ equals__________.
View SolutionThe system of linear equations x+λy−z=0, λx−y−z=0, x+y−λz=0 has a non-trivial solution for :
(1) infinitely many values of λ
(2) exactly one value of λ
(3) exactly two values of λ
(4) exactly three values of λ
View Solution
