If the equation $∣ ∣ x^{2} + b x + c ∣ ∣ = k$ has four real roots, then $b^{2} - 4 c > 0 a n d 0 < k < \frac{4 c - b^{2}}{4}$ $b^{2} - 4 c < 0 a n d 0 < k < \frac{4 c - b^{2}}{4}$ $b^{2} - 4 c > 0 a n d k > \frac{4 c - b^{2}}{4}$ none of these

Video Solution

Text Solution

Verified by Experts

We have $∣ ∣ x^{2} + b x + c ∣ ∣ = k$
For the equation to have four real roots, the line y=k must intersect $y = ∣ ∣ x^{2} + b x + c ∣ ∣$ at four points, which is not possible if $D = 0 or D < 0$ as the possible graphas of $y = ∣ ∣ x^{2} + b x + c ∣ ∣$ will be as follows.

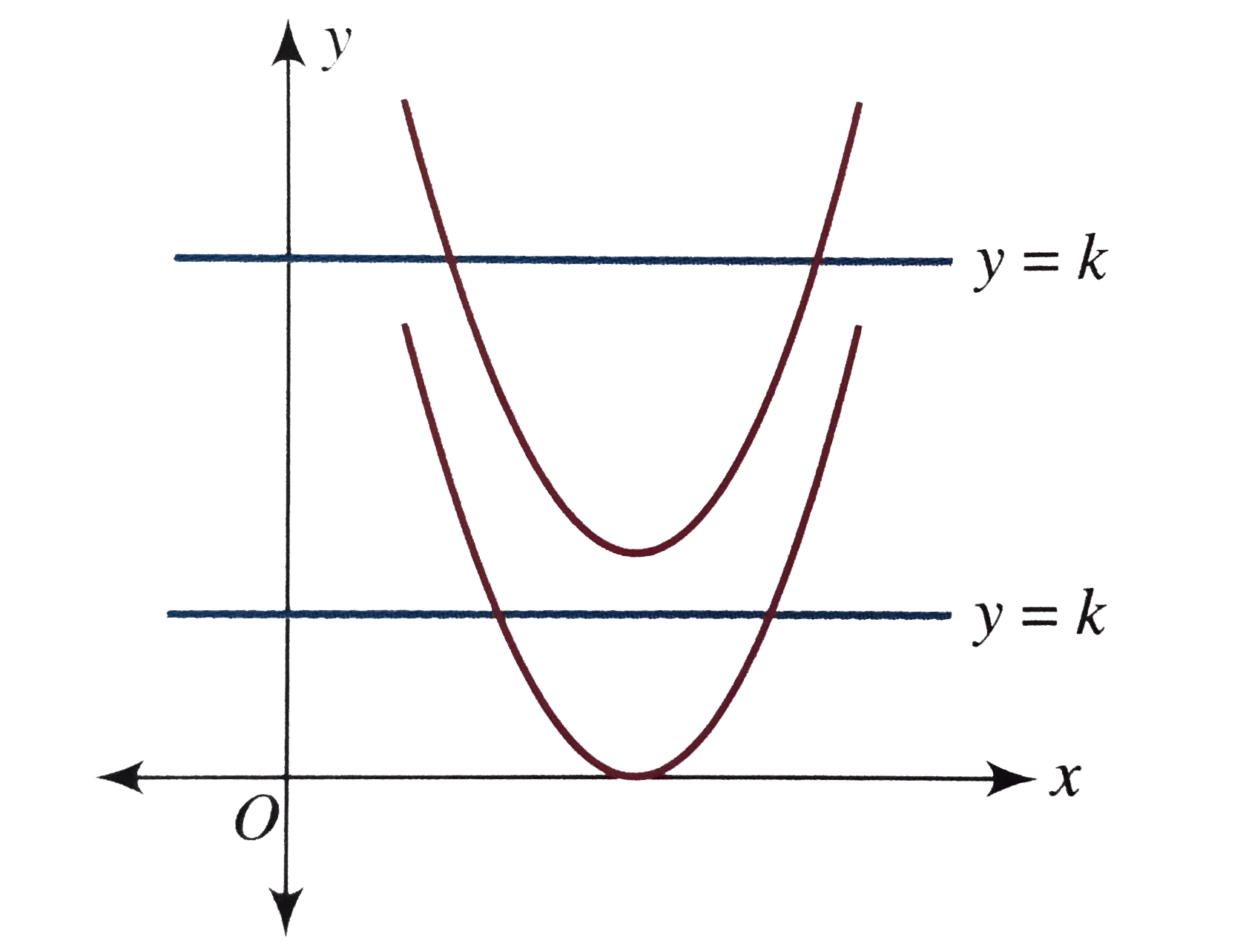
For the above graphs, the equation $∣ ∣ x^{2} + b x + c ∣ ∣ = k$ can have maximum two real roots. So for four real roots, we must have $D > 0$ , so the graph of $y = x^{2} + b x + c$ is as follows.

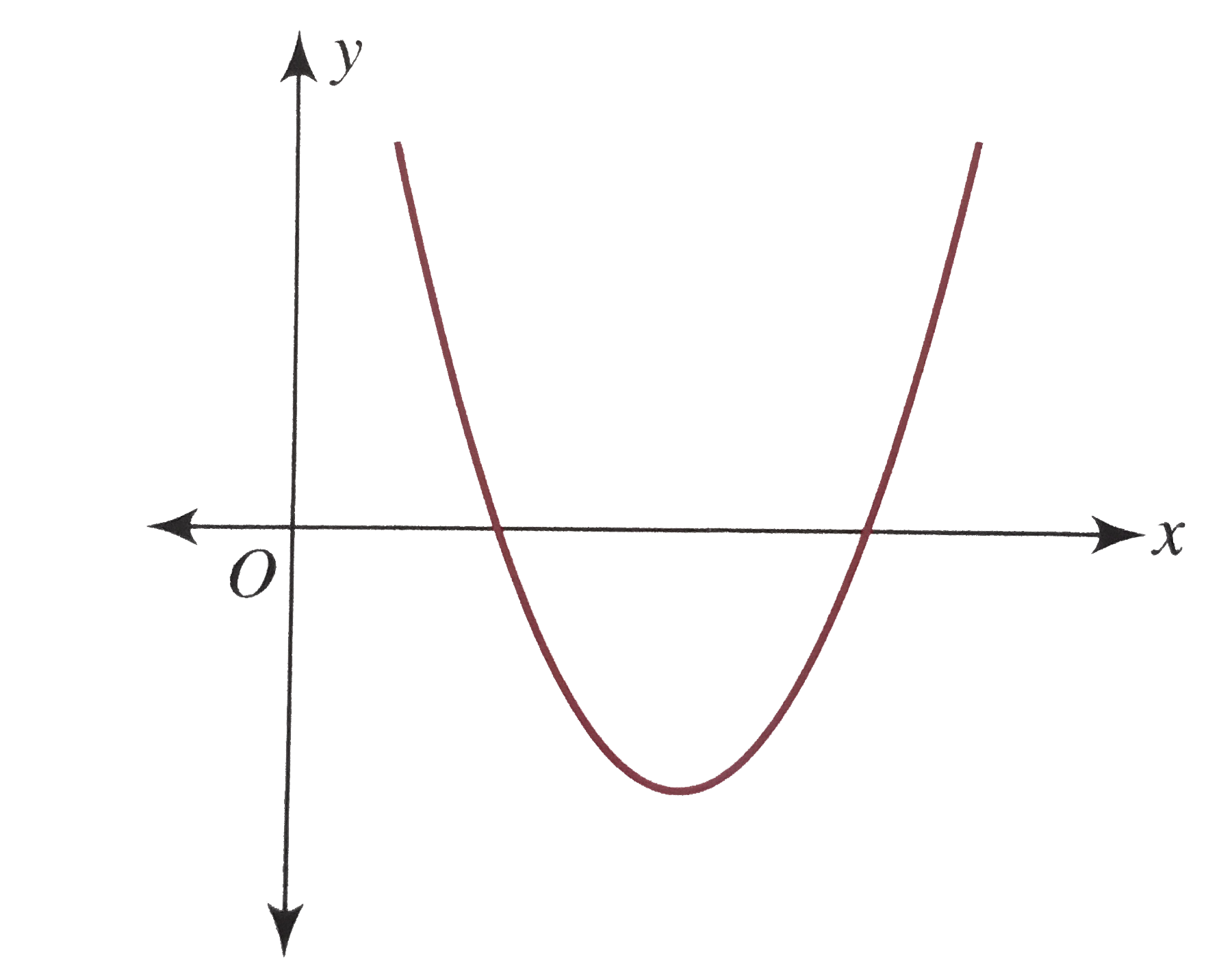
So the graph of $y = ∣ ∣ x^{2} + b x + c ∣ ∣$ will be as follows.

Now the equation $∣ ∣ x^{2} + b x + c ∣ ∣ = k$ will have four real if the line y=k intersects the above graph between the x-axis and point A.
Hence we have $0 < k < \frac{4 c - b^{2}}{4}$
Also $D > 0 ∴ b^{2} - 4 c > 0$ .

Updated on:21/07/2023

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the equation $a x^{2} + 2 b x - 3 c = 0$ has no real roots and $\frac{3 c}{4} < a + b$ , then
A $c < 0$
B $c > 0$
C $c \geq 0$
D $c = 0$

CENGAGE-GRAPHICAL TRANSFORMATIONS-Exercise

Home
Ask Doubt
Profile