If the graph of a function f(x is symmetrical about the line x = a, then
A
f(a+x)=f(a−x)
B
f(a+x)=f(x−a)
C
f(x)=f(−x)
D
none of these
Video Solution
Text Solution
The correct Answer is:A
Trivial
|
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Exercise
95 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
60 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
65 Videos
Similar Questions
Knowledge Check
The graph of the function y=f(x) is symmetrical about the line x=2, then :
Af(x+2)=f(x−2)Bf(2+x)=f(2−x)Cf(x)=f(−x)Dnone of theseThe graph of the function y=f(x) is symmetrical about the line x=2, then :
Af(x+2)=f(x-2)Bf(2+x)=f(2-x)Cf(x)=f(-x)Dnone of theseIf the function f(x) is symmetric about the line x=3, then the value of the integral I=∫8−2f(x)f(x)+f(6−x)dx is
A0B5C10D16
If the graph of y=f(x) is symmetrical about the lines x=1andx=2, then which of the following is true? (a)f(x+1)=f(x) (b) f(x+3)=f(x) (c)f(x+2)=f(x) (d) None of these
View SolutionIf the graph of y=ax3+bx2+cx+d is symmetric about the line x=K then the value of a+K is (y is not a constant function)
View SolutionConsider that the graph of y=f(x) is symmetrie about the lines x=2andx=4 then the period of f(x) is
View Solution83. A non-zero function f (x) is symmetrical about the line y=x then the value of λ (constant) such that f2(x)=(f−1(x))2−λxf(x)f−1(x)+3x2f(x) where all x∈R+
View SolutionIf the graph of the function
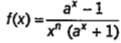 is symmetric about y-axis, then n is equal to :
is symmetric about y-axis, then n is equal to :
View Solution
