If the graph of the function y = f(x) is symmetrical about the line x = 2, then
f(x)=f(−x)
f(2+x)=f(2−x)
f(x+2)=f(x−2)
f(x)=−f(−x)
The correct Answer is:B
Step by step video, text & image solution for If the graph of the function y = f(x) is symmetrical about the line x = 2, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - QUESTIONS FROM PREVIOUS YEAR.S B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
19 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EXERCISE (NUMERICAL ANSWER TYPE QUESTIONS )
20 Videos
- QUADRATIC EQUATIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Questions from previous Years. B - architecture entrance examination papers
16 Videos
- STATISTICS BOOK - MCGROW HILL PUBLICATIONCHAPTER - STATISTICS EXERCISE - QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
13 Videos
Similar Questions
Knowledge Check
If the graph of a function f(x is symmetrical about the line x = a, then
Af(a+x)=f(a−x)Bf(a+x)=f(x−a)Cf(x)=f(−x)Dnone of theseIf the garph of the function f(x)=ax3+x2+bx+c is symmetric about the line x = 2, then the value of a+b is equal to
A10B−4C16D−10If the function f(x) is symmetric about the line x=3, then the value of the integral I=∫8−2f(x)f(x)+f(6−x)dx is
A0B5C10D16
If the graph of y=f(x) is symmetrical about the lines x=1andx=2, then which of the following is true? (a)f(x+1)=f(x) (b) f(x+3)=f(x) (c)f(x+2)=f(x) (d) None of these
View SolutionIf the graph of the function
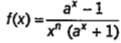 is symmetric about y-axis, then n is equal to :
is symmetric about y-axis, then n is equal to :
View SolutionThe graph of the function f(x)=−2−|x|
View SolutionIf f(x)=f(2a−x) then the graph of f(x) is symmetric about the line
View SolutionIf the graph of y=ax3+bx2+cx+d is symmetric about the line x=K then the value of a+K is (y is not a constant function)
View Solution
