If the length of the tangent from (5,4) to
the circle x2+y2+2ky=0 is 1 the n find k. Solution in Telugu
Step by step video & image solution for If the length of the tangent from (5,4) to the circle x^(2) + y^(2) + 2ky = 0 is 1 the n find k. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - CIRCLES(SHORT ANSWER TYPE QUESTIONS)
6 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - CIRCLES(LONG ANSWER TYPE QUESTIONS)
13 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - RANDOM VARIABLES & PROBABILITY DISTRIBUTIONS (LONG ANSWER TYPE QUESTIONS)
6 Videos
- MODEL PAPER 9 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 9 EXERCISE - SECTION-C (III. LONG ANSWER TYPE QUESTIONS)
7 Videos
Similar Questions
If a point P is moving such that the lengths of tangents drawn from P to the circles
x2+y2−4x−6y−12=0 and
x2+y2+6x+18y+26=0 are the ratio 2:3, then find the equation to the locus of P.
View SolutionFind the equation of the circle passing through the points
(3,4)(3,2),(1,4)
View SolutionThe probability distribution of a random variable X is given below.
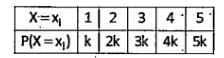
Find the value of k, mean, also find variance of X.
View SolutionIf n is a positive integer, show that
(P+iQ)1/n+(P−iQ)1/n=2(P2+Q2)1/2ncos(1n,tan.QP).
View SolutionIf the length of the tangent from (5,4) to
the circle x2+y2+2ky=0 is 1 the n find k.
View SolutionIf the circles x2+y2+2x+2ky+6=0 and x2+y2+2ky+k=0 intersect orthogonally , then k is equal to _
View SolutionThe length of the tangent from the point (-1,1) to the circle x2+y2−4x+k=0 equal to 2 then k=
View SolutionIf the length of the tangent from (2,3) to circle x2+y2+6x+2ky−6=0 is equal to 7.
View SolutionIf the length of the tangent from (h,k) to the circle x2+y2=16 is twice the length of the tangent from the same point to the circle x2+y2+2x+2y=0, then
View SolutionThe length of the common chord of the circles x2+y2+2hx=0,x2+y2−2ky=0 is
View Solutionयदि वृत्त x2+y2−6x+2ky−25=0 की त्रिज्या √50 हो , तो k का मान ज्ञात कीजिए ।
View SolutionFind the lengths of the tangents drawn from the point.
(−1,1) to the circle x2+y2−2x+4y+1=0
View SolutionIf the circles x2+y2+2x+2ky+6=0 and x2+y2+2ky+k=0 intersect orthogonally , then k is :
View SolutionFind the length of the common chord of the circle x2+y2+2hx+a2=0 and x2+y2−2ky−a2=0.
View SolutionIf the circles x2+y2+2x+2ky+6=0 and x2+y2+2ky+k=0 intersect orthogonally, show that k=2 or -3/2
View SolutionIf the length of the tangent from (5,4) to
the circle x2+y2+2ky=0 is 1 the n find k.
View Solution
