If the line x=y=z intersect the line s∈A.x+s∈B.y+s∈C.z=2d2,s∈2A.x+s∈2B.y+s∈2C.z=d2, then find the value of sinA2.sinB2.sinC2whereA,B,C are the angles of a triangle.
Any point on the line x=y=z is (λ,λ,λ)
This point lies on the planes
sinA⋅x+sinB⋅y+sinC⋅z=2d2
and sin2A⋅x+sin2B⋅y+sin2C⋅z=d2
∴ sinAλ+sinBλ+sinCλ=2d2
and sin2Aλ+sin2Bλ+sin2Cλ=d2
Eliminating d2, we get
sinA+sinB+sinC=2(sin2A+2sin2B+sin2C)
or 4cosA2cosB2cosC2=8sinAsinBsinC
or sinA2sinB2sinC2=116
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.112videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.215videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank34videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
The lines 3x+4y=9&4x−3y+12=0 intersect at P. The first line intersects x−aξs at A and the second line intersects y−aξs at B. Then the circumradius of the triangle PAB is 32 (b) 52 (c) 10 (d) none
View SolutionIf asinA=K, then the area of DeltaA B C in terms of K and sines of the angles is K24s∈A s∈B s∈C (b) K22s∈A s∈B s∈C 2K2s∈A s∈B sin(A+B) (d) none
View Solution
Knowledge Check
- Question 1 - Select One
In ΔABCif2s=a+b+cand(s−b)(s−c)=x sin2A2 ,then the value of x is
AbcBcaCabDabc - Question 2 - Select One or More
If the cosine of the angle between the lines having d.R.s 1,−1,2 and 0,1,a is √32, then: a=
A2,6B−2.−6C1,7D−1,−7 - Question 3 - Select One
The distance between the lines
x=1−4t,y=2+t,z=3+2t and x=1+s,y=4−2s,z=−1+s isA8B16/√90C8/√5D16/√110
In a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionLet ABC be a triangle right-angled at AandS be its circumcircle. Let S1 be the circle touching the lines AB and AC and the circle S internally. Further, let S2 be the circle touching the lines AB and AC produced and the circle S externally. If r1 and r2 are the radii of the circles S1 and S2 , respectively, show that r1r2=4 area (ABC).
View SolutionIn the shown fig. S1 and S2 are two identical coher- ent sources of sound, separated by a distance d. A receiver moves along the line XY (which is parallel to line S1 S2) to detect the intensity of sound at various points on the line. Distance of line XY from line S1 S2 isD(>>d). Point O is the foot of perpendicular bisector of the line S1 S2 on XY. Distance of first intensity maxima (on line XY) measured from O is y. Find percentage change in value of y if the temperature of air increases by 1%.
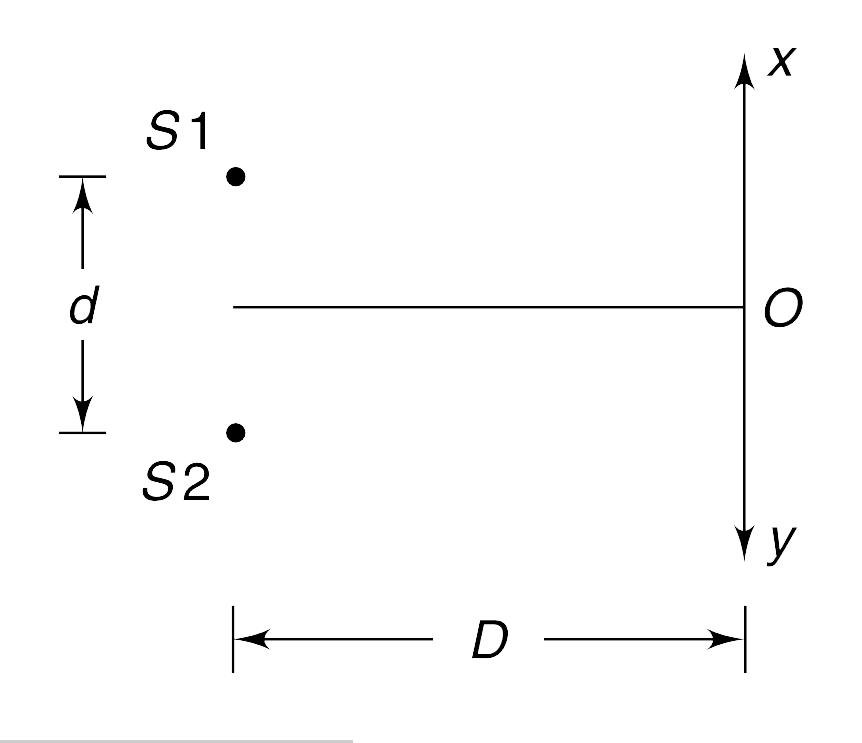 View Solution
View SolutionIf a + b+ c =2s , thent the value of (s−a)2+(s−b)2+(s−c)2 will be
View SolutionIn △ABC,sin(A2)sin(C2)=sin(B2) and '2s' is the perimeter of the triangle. Then the value of s is
View Solution

