If the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the monor axis, then prove that eccentricity is constant.
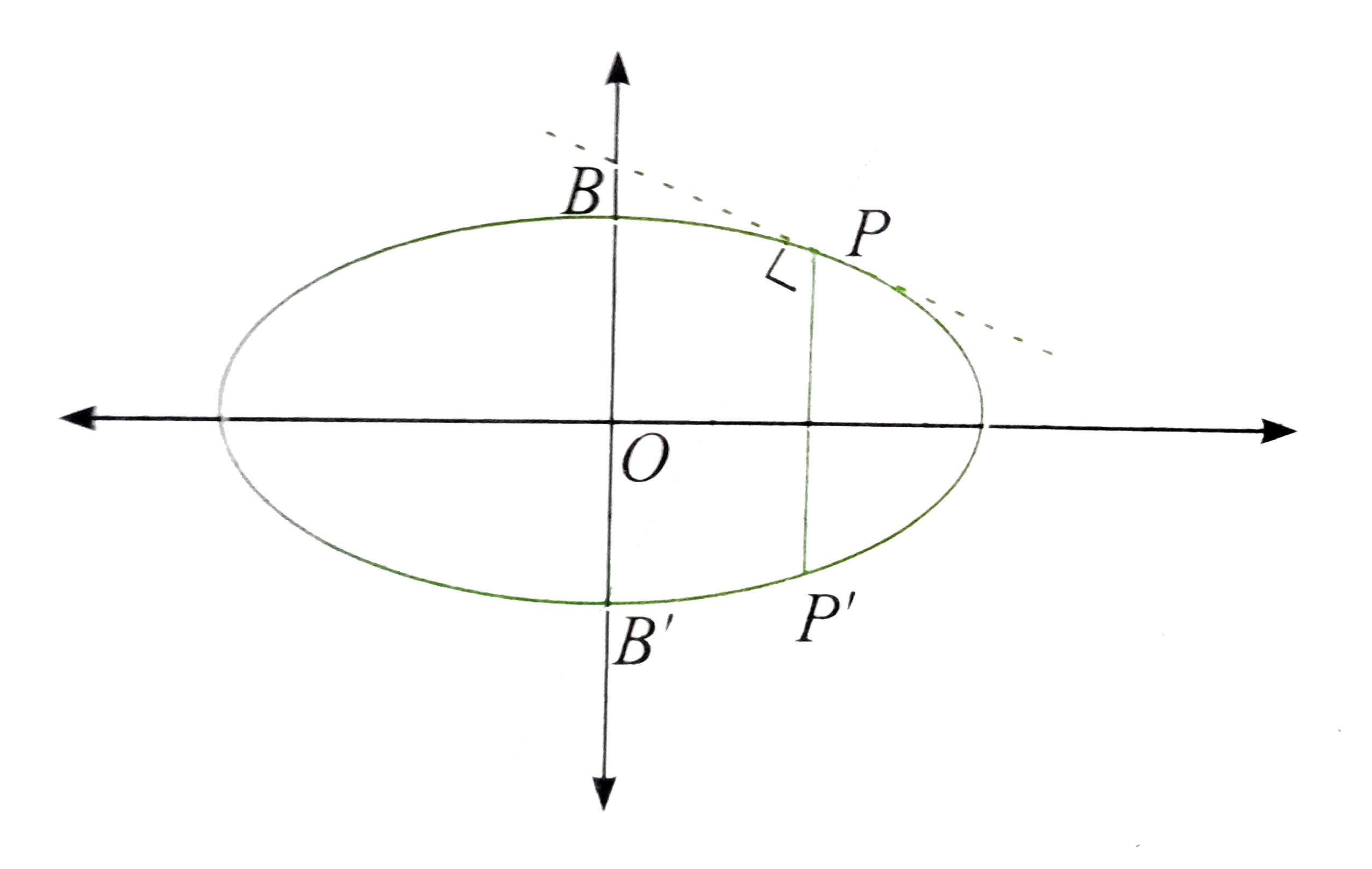
The equation of the normal at the extermity P of latus reactum is x−ey=ae3
This passes through the extermity of the minor i.e.,B'(0,-b).
Then, 0+eb−ae3=0
orba2 orb2=a2e4
or a2(1−e2)=a2e4 ore4+e2−1=0
Similar Questions
If the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the minor axis, then prove that eccentricity is constant.
View SolutionIf the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the minor axis, then prove that eccentricity is constant.
View Solution
Knowledge Check
If the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the monor axis, then prove that eccentricity is constant.
Ae4−e2+1=0Be2−e+1=0Ce2+e+1=0De4+e2−1=0If the normal at an end of latus rectum of the hyperbola x2a2−y2b2=1 passes through the point (0,2b) then
Aeccentricity of the hyperbola is 1+√22Beccentricity of the hyperbola is √2Csquare of the eccentricity is 2 times the ratio of transverse and conjugate axisDratio of transverse and conjugate axis is unity
The normal at an end of a latus rectum of the ellipse x2a2+y2b2=1 passes through an end of the minor axis if:
View SolutionThe normal at an end of a latus rectum of the ellipse x2a2+y2b2=1 passes through an end of the minor axis if
View SolutionThe normal at an end of a latus rectum of the ellipse x2a2+y2b2=1 passes through an end of the minor axis if
View SolutionIf the normal at an end of a latus-rectum of an elipse x2a2+y2b2=1 passes through one extremity of the minor axis, show that the eccentricity of the ellipse is given by e4+e−1=0
View SolutionIf the normal at an end of a latus-rectum of an ellipse x2a2+y2b2=1 passes through one extremity of the minor axis, show that the eccentricity of the ellipse is given by e=√√5−12
View SolutionIf the normal at an end of latus rectum of the hyperbola x2a2−y2b2=1 passes through the point (0,2b) then
View Solution
