If the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the monor axis, then prove that eccentricity is constant.Solution in Bengali
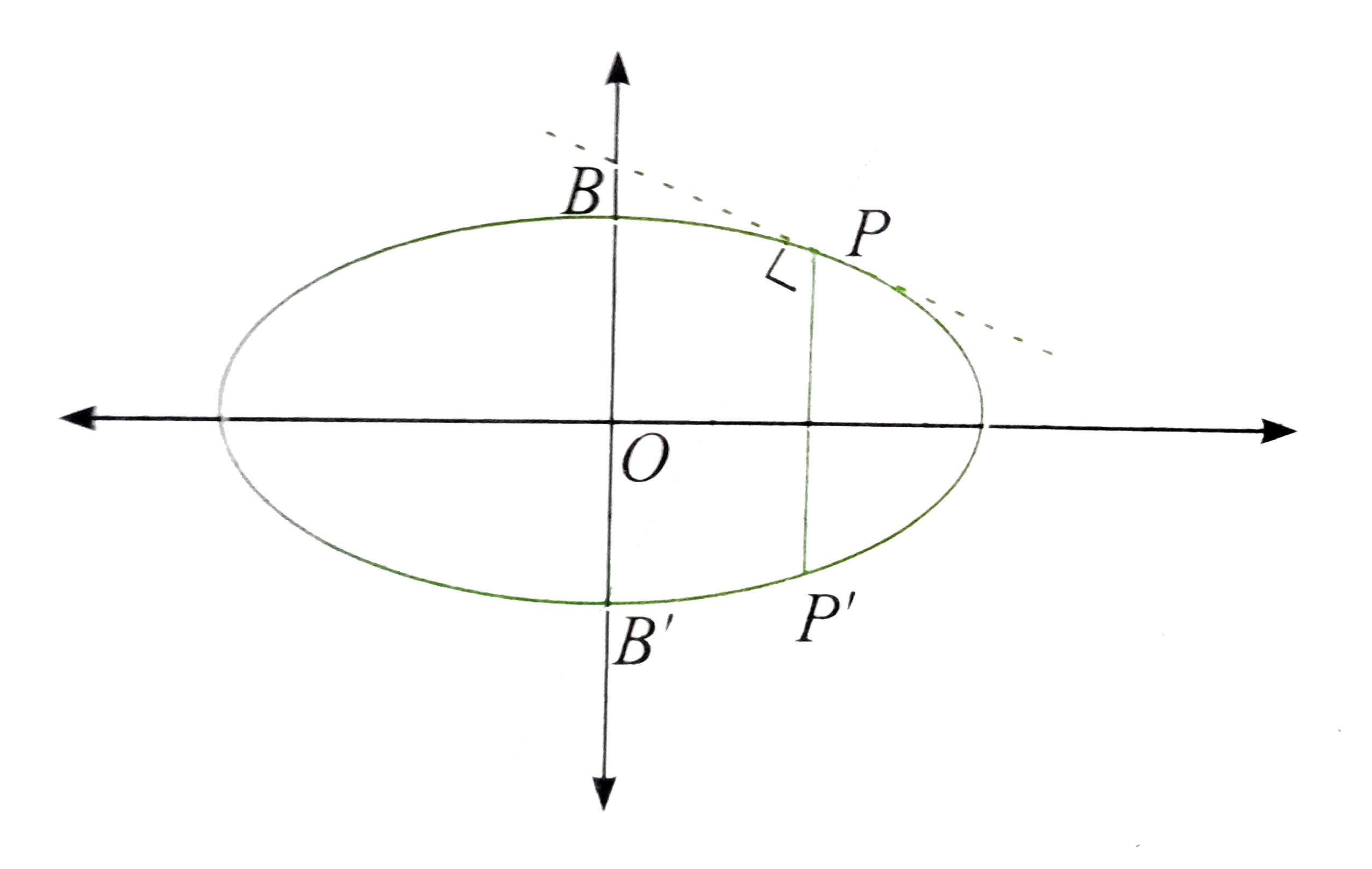
The equation of the normal at the extermity P of latus reactum is x−ey=ae3
This passes through the extermity of the minor i.e.,B'(0,-b).
Then, 0+eb−ae3=0
orba2 orb2=a2e4
or a2(1−e2)=a2e4 ore4+e2−1=0
Similar Questions
If the normal drawn at one end of the latus rectum of the ellipse b2x2+a2y2=a2b2 with eccentricity 'e' passes through one end of the minor axis. Then,
View SolutionIf the normal drawn at one end of the latus rectum of the ellipse b2x2+a2y2=a2b2 with eccentricity 'e' passes through one end of the minor axis. Then,
View SolutionIf the normal at one end of lotus rectum of an ellipse passes through one end of minor axis then prove that,
e4+e2−1=0
View SolutionIf the normal at one end of lotus rectum of an ellipse passes through one end of minor axis then prove that,
e2=√5−12, where e is the eccentricity of the ellipse.
View SolutionThe normal at an end of a latus rectum of the ellipse x2a2+y2b2=1 passes through an end of the minor axis if:
View SolutionIf the normal at one end of latusrectum of an ellipse x2a2+y2b2=1 passes through one end of minor axis then
View SolutionIf the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the minor axis, then prove that eccentricity is constant.
View SolutionIf the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the monor axis, then prove that eccentricity is constant.
View Solution
