If the normal at P(23√32) meets the major axis of ellipse x216+y29=1 at Q , and S and S' are the foci of the given ellipse, then find the ratio SQ:S′Q.
Equatio of ellipse P(2,3√32)
∴e2=1−916+716
⇒e=√74
Hence , foci are S(√7,0)andS(−√7)
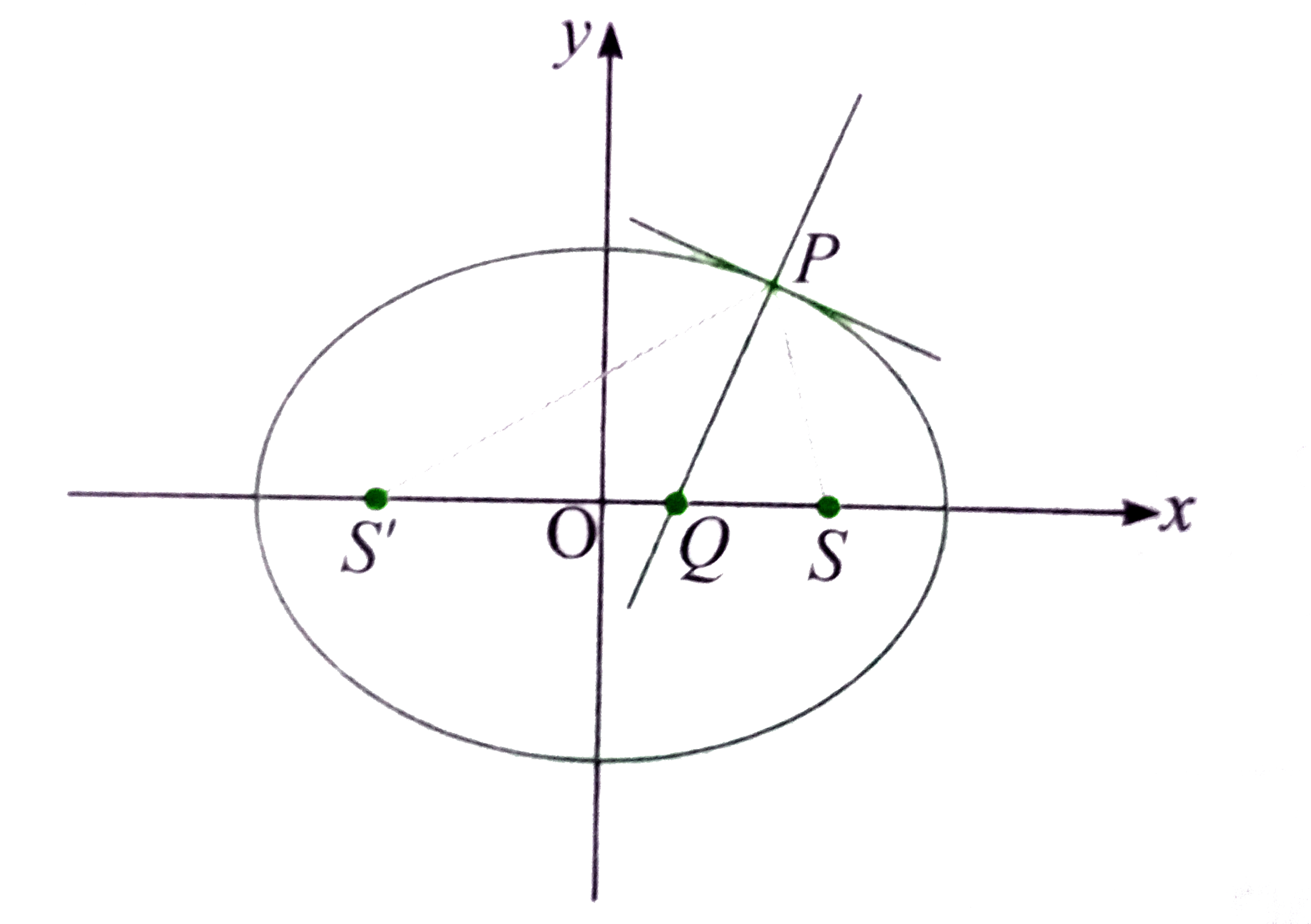
Normal at P bisects the angle ∠SPS''
Therefore, in triangle SPS' using bisector theorem, we get SQS'Q=SPS'P=a−exa+ex=4−√74×24+√74×2=8−√78−√7
Similar Questions
Knowledge Check
- Question 1 - Select One
The length of the major axis of the ellipse
(x−3)216+(y+2)225=1 isA3B4C6D10
The foci of the ellipse (x−3)236+(y+2)216=1, are
View SolutionLet P be a point on the ellipse x2a2+y2b2=1 of eccentricity e. If A,A' are the vertices and S,S are the foci of the ellipse, then find the ratio area PSS'' : area APA′.
View SolutionLet P any point on ellipse 3x2+4y2=12 . If S and S'' are its foci then find the the locus of the centroid of trianle PSS''
View SolutionLet P be a variable point on the ellipse x225+y216=1 with foci at S and S'. Then find the maximum area of the triangle SPS'
View SolutionIf P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
View SolutionLet S, S' be the focil and BB' be the minor axis of the ellipse x2a2+y2b2=1. If ∠BSS'=θ, then the eccentricity e of the ellipse is equal to
View SolutionNormal to the ellipse x264+y249=1 intersects the major and minor axes at PandQ , respectively. Find the locus of the point dividing segment PQ in the ratio 2:1.
View Solution

