If the point of intersection of more than and less than ogiven is (20.5, 30.7) then the median is _______
The correct Answer is:20.5
To find the median given the point of intersection of the more than and less than curves, we can follow these steps:
1. Understand the Given Information:
We are given that the point of intersection of the more than and less than curves is (20.5, 30.7). This means that at x = 20.5, the cumulative frequency of the data is 30.7.
2. Identify the Median:
The median is the value that separates the higher half from the lower half of the data set. In the context of cumulative frequency curves, the median corresponds to the x-coordinate of the point where the cumulative frequency reaches half of the total frequency.
3. Locate the x-coordinate:
From the point of intersection (20.5, 30.7), we see that the x-coordinate is 20.5. This x-coordinate represents the median of the data set.
4. Conclusion:
Therefore, the median of the given data set is 20.5.
Final Answer:
The median is 20.5.
---
We are given that the point of intersection of the more than and less than curves is (20.5, 30.7). This means that at x = 20.5, the cumulative frequency of the data is 30.7.
The median is the value that separates the higher half from the lower half of the data set. In the context of cumulative frequency curves, the median corresponds to the x-coordinate of the point where the cumulative frequency reaches half of the total frequency.
From the point of intersection (20.5, 30.7), we see that the x-coordinate is 20.5. This x-coordinate represents the median of the data set.
Therefore, the median of the given data set is 20.5.
The median is 20.5.
Topper's Solved these Questions
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Short Answer Type Question (I)
9 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Short Answer Type Question (II)
8 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-D)
1 Videos
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-D)
1 Videos
Similar Questions
Q10. What is the median of the more than and less than type ogives if the coordinates of the point of intersection of the two graphs are (20.5, 29) 211. Draw more than type ogive and find the median. Also verify it using formula. C50-55 55 60 60- 65 65- 70 70-75 75-80 f→ 2 6 8 14 15 5
View SolutionSet of multiples of 5 which are more than 100 and less than 125.
View Solution
Knowledge Check
2 less than −7 is
A−9B-5C5Dnone of theseThe abscissa of the point of intersection of the less that type of the more than type cumulative frequency curves of a grouped data gives its
AmeanBmedianCmodeDAll of theseIf the 'less than type' ogive and 'more than type' ogive intersect each other at (20.5, 15.5) then the median of the given data is
A5.5B15.5C20.5D36
The point where ' less than ogive' and more than ogive ' intersect each other determines median .
View Solution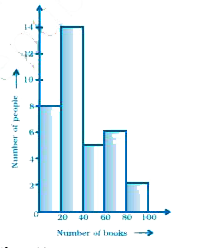
The number of people having books more than 20 and less than 40 is ________.
View SolutionFor a given data with 70 observations the less then ogive and the more than ogive intersect at (20.5,35). The median of the data is 20 (b) 35 (c) 70 (d) 20.5
View SolutionWhich measure of central tendency is given by the x -coordinate of the point of intersection of the more than ogive and less than ogive?
View SolutionIf x is 20% more than y then y is __ % less than x
View Solution
