If the points (x,y) are equidistant from the points (a+b,b-a) and (a-b,a+b),prove that bx = ay.Solution in Odia
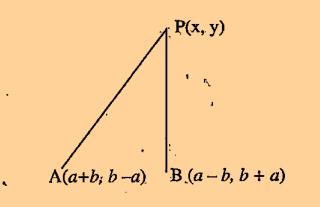
Given that ¯¯¯¯¯¯AP=¯¯¯¯¯¯BP
∴√(x−a−b)2+(y−b+a)2 ,
= √(x−a+b)2+(y−b+a)2
or, x2+a2+b2−2ax+2ab−abx+y2+b2+a2−2by−2ab−2ay
= x2+a2+b2−2ax−2ab−2by
or, 4bx = 4ay or, bx = ay .
Topper's Solved these Questions
Similar Questions
If the values observed are 1,2,…..,n each with frequency 1, find the mean value
View SolutionThe number of lines making equal angles with coordinate axes is_____.
View SolutionIf the point P(x,y) is equidistant from the points A(a+b,b-a) and B(a-b,a+b). Prove that bx=ay.
View SolutionIf the point (x,y) is equidistant from the points (a+b,b−a) and (a−b,a+b) , prove that bx=ay
View SolutionIf the point P(x,y) be equidistant from the points A(a+b,b-a) and B(a-b,a+b), then prove that bx=ay
View SolutionIf the point P(x,y) be equidistant from the points A(a+b,b-a) and B(a-b,a+b), then prove that bx=ay
View SolutionIf the point (x;y) is equidistant from the points (a+b;b−a) and (a−b;a+b) prove that bx=ay
View SolutionIf the point (x, y) is equidistant from the points (a+b, b-a) and (a-b, a+b), then prove that bx=ay.
View Solutionयदि बिन्दु P(x,y) बिन्दुओ A(a+b,b−a) और B(a−b,a+b) से समदूरस्थ है , तो सिद्ध कीजिए कि bx=ay.
View Solutionयदि बिन्दु (x, y) दो बिन्दुओं (a+b,b−a) और (a−b),a+b) से समान दूरी पर हों , तो दर्शाइए कि bx=ay होगा ।
View Solutionयदि बिंदु (x, y) बिन्दुओ (a + b, b - a) और (a - b, a + b) से समान दूरी पर स्थित है, तो सिध्द कीजिए की bx = ay.
View SolutionIf the point (x,y) be equidistant from the points (a+b,b-a) and (a-b,a+b) , prove that bx =ay .
View SolutionIf the point (x,y) be equidistant from the points ( a+b, b-a) and (a-b, a+b) then prove that bx=ay.
View Solution(x,y) বিন্দু (a+b,b−a) ও (a−b,a+b) বিন্দু দুটি থেকে সমদূরবর্তী হলে প্রমাণ করো যে, bx=ay
View SolutionIf distances of a point (x, y) are equidistant from (a +b, b-a) and (a- b, a + b), prove that bx = ay.
View SolutionIf the point P (x, y) is equidistant from the points A (a + b, b - a) and B(a -b, a + b). Prove that bx = ay.
View Solution
