If the radius of the circumcircle of the triangle TPQ, where PQ is chord of contact corresponding to point T with respect to circle x2+y2−2x+4y−11=0, is 6 units, then minimum distances of T from the director circle of the given circle is
A
6
B
12
C
6√2
D
12−4√2
Video Solution
Text Solution
The correct Answer is:4
Given circle (x−1)2+(y+2)2=16
Its director circle is
(x−1)2+(y+2)2=32
∴OS=4√2
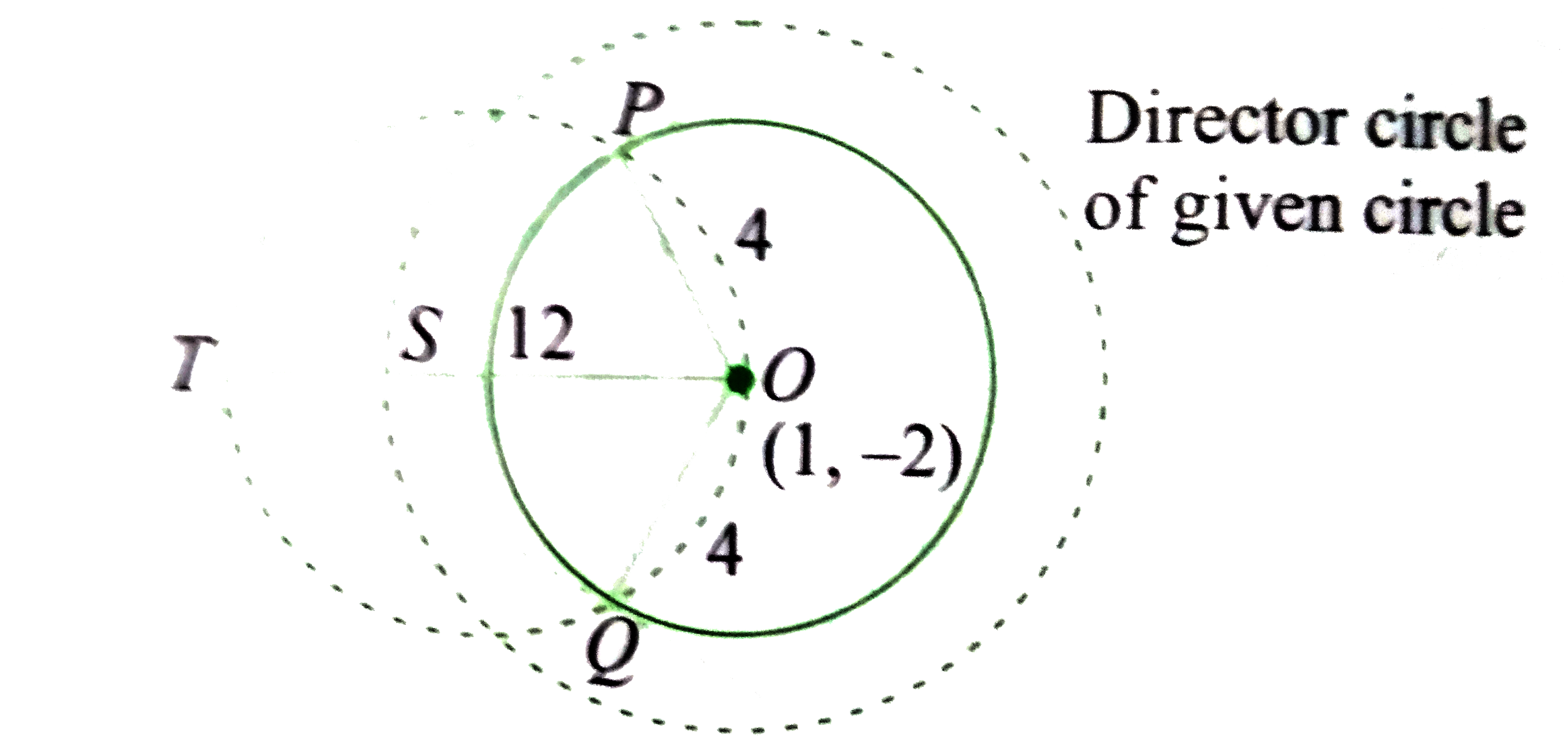
Therefore, required distance,
TS=OT−SO=12−4√2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
The point on the circle x2+y2−2x−4y−11=0 which is farthest from the origin is
A(1+8√5,2+4√5)B(1+4√5,2+8√5)C(2+8√5,1+4√5)Dnone - Question 2 - Select One
If a chord of contact of tangents drawn from a point P with respect to the circle x2+y2=9 is x=2, then area, in square units, of triangle formed by tangents drawn from P to the circle and their chord of contact is equal to
A4√52B9√32C5√5)2Dnone of these
Find the equation of the chord of contact of the point (1,2) with respect to the circle x2+y2+2x+3y+1=0
View SolutionThe point on the circle x2+y2−6x+4y−12=0 which is at maximum distance from the point (−9,7) is
View SolutionDiscuss the position of the points (1,2) and (6,0) with respect to the circle x2+y2−4x+2y−11=0
View SolutionThe inverse point of (2,-3) W.r.t to circle x2+y2+6x−4y−12=0 is
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View SolutionFind the length of the chord of contact with respect to the point on the director circle of circle x2+y2+2ax−2by+a2−b2=0 .
View Solution

