If the standard deviation of the binomial distribution (q+p)16 is 2, then mean of the distribution is
6
8
10
12
The correct Answer is:B
To solve the problem, we need to find the mean of a binomial distribution given that the standard deviation is 2. Let's break this down step by step.
Step 1: Understand the standard deviation of a binomial distribution
The standard deviation (SD) of a binomial distribution is given by the formula:
SD=√n⋅p⋅q
where:
- n is the number of trials,
- p is the probability of success,
- q is the probability of failure, and q=1−p.
Step 2: Use the information given in the problem
From the problem, we know:
- The standard deviation is 2.
- The expression for the binomial distribution is (p+q)16, which indicates n=16.
Step 3: Set up the equation for standard deviation
Since the standard deviation is given as 2, we can square it to eliminate the square root:
22=n⋅p⋅q
This simplifies to:
4=16⋅p⋅(1−p)
Step 4: Simplify the equation
Now, we simplify the equation:
4=16p(1−p)
Dividing both sides by 16 gives:
416=p(1−p)
This simplifies to:
14=p(1−p)
Step 5: Rearranging the equation
We can rearrange the equation:
p−p2=14
Rearranging gives us a quadratic equation:
p2−p+14=0
Step 6: Solve the quadratic equation
To solve for p, we can use the quadratic formula:
p=−b±√b2−4ac2a
Here, a=1, b=−1, and c=14:
p=−(−1)±√(−1)2−4⋅1⋅142⋅1
This simplifies to:
p=1±√1−12=1±02=12
Step 7: Find the mean of the distribution
The mean of a binomial distribution is given by:
Mean=n⋅p
Substituting n=16 and p=12:
Mean=16⋅12=8
Final Answer
Thus, the mean of the distribution is:
8
The standard deviation (SD) of a binomial distribution is given by the formula:
SD=√n⋅p⋅q
where:
- n is the number of trials,
- p is the probability of success,
- q is the probability of failure, and q=1−p.
From the problem, we know:
- The standard deviation is 2.
- The expression for the binomial distribution is (p+q)16, which indicates n=16.
Since the standard deviation is given as 2, we can square it to eliminate the square root:
22=n⋅p⋅q
This simplifies to:
4=16⋅p⋅(1−p)
Now, we simplify the equation:
4=16p(1−p)
Dividing both sides by 16 gives:
416=p(1−p)
This simplifies to:
14=p(1−p)
We can rearrange the equation:
p−p2=14
Rearranging gives us a quadratic equation:
p2−p+14=0
To solve for p, we can use the quadratic formula:
p=−b±√b2−4ac2a
Here, a=1, b=−1, and c=14:
p=−(−1)±√(−1)2−4⋅1⋅142⋅1
This simplifies to:
p=1±√1−12=1±02=12
The mean of a binomial distribution is given by:
Mean=n⋅p
Substituting n=16 and p=12:
Mean=16⋅12=8
Thus, the mean of the distribution is:
8
Topper's Solved these Questions
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Solved Examples (Numerical Answer )
21 Videos
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Exercises (Single Correct Answer)
10 Videos
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Solved Examples (Level 1 Single Correct )
80 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
17 Videos
- PROGRESSIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
25 Videos
Similar Questions
Knowledge Check
The mean deviation of the following distribution is
 A11,5B0.75C1.25D26
A11,5B0.75C1.25D26The mean deviation of the following distribution is
 A11.5B0.75C1.25D26
A11.5B0.75C1.25D26The standard deviation of the following frequency distribution
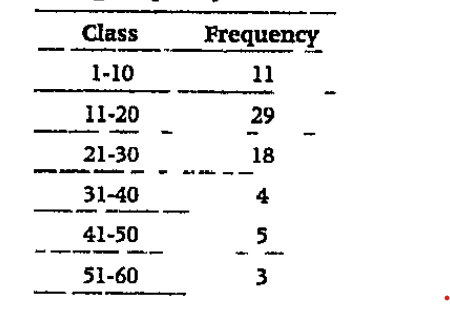 A12.7B13.6C15.3DNone of these
A12.7B13.6C15.3DNone of these
For a binomial distribution mean is 6 and S.D .is √2.The distribution is
View SolutionIf the mean and variance of a binomial distribution are respectively 9 and 6, find the distribution.
View SolutionIf the mean and variance of a binomial distribution are respectively 9 and 6, find the distribution.
View SolutionFind the standard deviation for the following frequency distribution
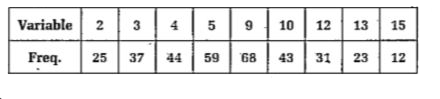
View SolutionThe mean and standard deviation of a binomial distribution are 12 and 2 respectively. What is the number of trials?
View Solution
