If the tangent at any point of the ellipse $\frac{x^{2}}{a^{3}} + \frac{y^{2}}{b^{2}} = 1$ makes an angle $α$ with the major axis and an angle $β$ with the focal radius of the point of contact, then show that the eccentricity of the ellipse is given by $e = \frac{cos β}{cos α}$

Video Solution

Text Solution

Verified by Experts

Let $P (a cos θ, b sin θ)$ be any point on the ellipse.
The equation of tangent at $P (θ)$ is
$\frac{x cos θ}{4} + (y sin θ) (b () = 1 (1)$
Tangent meets the major axis at $T (a sec θ, 0)$ .
Applying since rule in $Δ P S T$ , we get
$\frac{P S}{sin (π - α)} = \frac{S T}{sin β}$
$or \frac{1 - e cos θ}{sin α} = \frac{a (sec θ - e)}{sin β}$
or $cos θ = \frac{sin α}{sin β}$

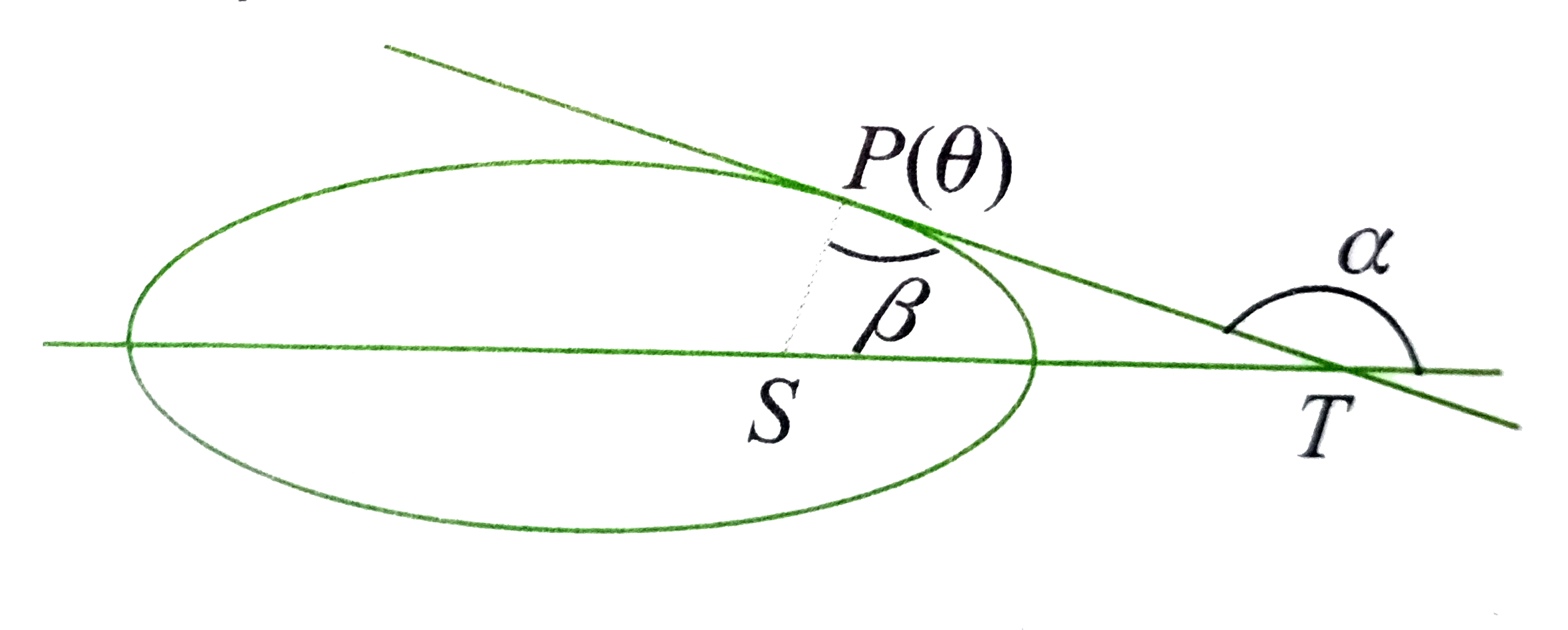
The slop of tangent is $- \frac{b}{a} cot θ = tan α$
$or \frac{b^{2}}{a^{2}} = {tan}^{2} α ({sec}^{2} θ - 1)$
$= {tan}^{2} α (\frac{{sin}^{2} β - sin α}{{cos}^{2} α})$
$= \frac{{sin}^{2} β - {sin}^{2} α}{{cos}^{2} α}$
$or e = \sqrt{1 - \frac{{sin}^{2} β - {sin}^{2} α}{{cos}^{2} α}}$
$= \sqrt{\frac{1 - {sin}^{2} β}{{cos}^{2} α}} = \frac{cos β}{cos α}$

Updated on:21/07/2023

If the tangents drawn from a point on the hyperbola $x^{2} - y^{2} = a^{2} - b^{2}$ to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ make angle $α$ and $β$ with the transverse axis of the hyperbola, then
A $tan α - tan β = 1$
B $tan α + tan β = 1$
C $tan α tan β = 1$
D $tan α tan β = - 1$
If the angle betweent he lines joining the end points of minor axis of an ellipse with its foci is $\frac{π}{2},$ then the eccentricity of the ellipse is
A $\frac{1}{2}$
B $\frac{1}{\sqrt{2}}$
C $\frac{\sqrt{3}}{2}$
D $\frac{1}{2 \sqrt{2}}$
If the distance of a point on the ellipse $\frac{x^{2}}{6} + \frac{y^{2}}{2} = 1$ from the centre is 2, then the eccentric angle of the point, is
A $\frac{π}{4}, \frac{3 π}{4}$
B $\frac{π}{3}, \frac{2 π}{3}$
C $π / 2$
Dnone of these