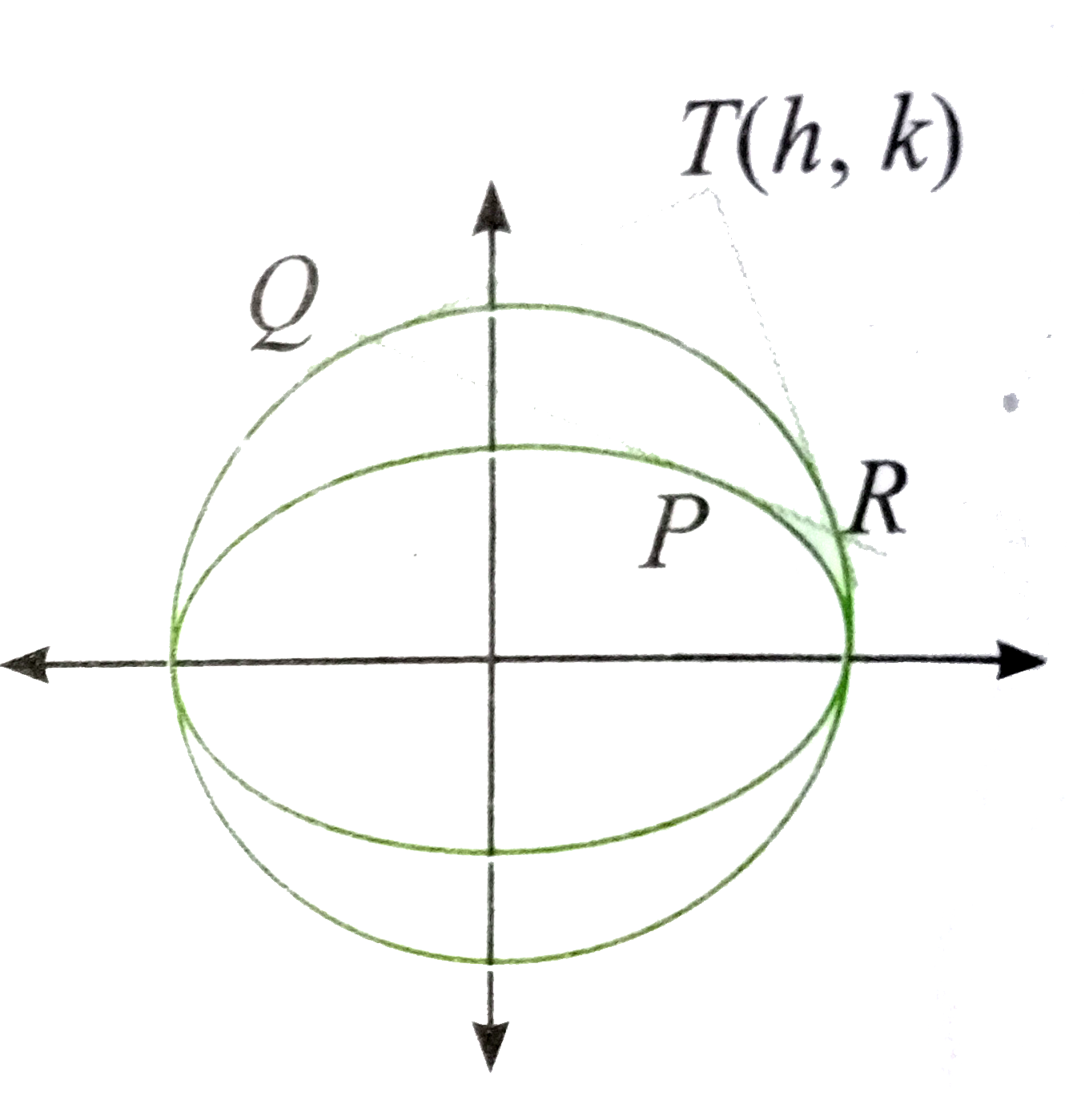
If the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.Solution in Bengali
The correct Answer is:(1,√2,1)
The equation of tangent to the ellipse at a given points is x(1√2)+2y(12)=1
or x+√y=√2 (1)
Now, QR is the chord of contact of the circle x2_y2=1 with respect to the point T(h,k). Then,
QR≡hx+ky+ky=1 (2)
Equations (1) and (2) represent the same straight line. Then comapring the ratio of coefficients, we have, h/1=k/√2=1√2.
Hence (h,k)≡(1/√2)
Similar Questions
The straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionThe point of intersection of the tangents at the point P on the ellipse x2a2+y2b2=1 and its corresponding point Q on the auxiliary circle meet on the line (a) x=ae (b) x=0 (c) y=0 (d) none of these
View SolutionA variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P व Q बिन्दुओं पर मिलती है। सिद्ध कीजिए कि P व Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें लम्बवत् होंगी।
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionIf the tangent to the ellipse x^2+2y^2=1 at point P(1/(sqrt(2)),1/2) meets the auxiliary circle at point R and Q , then find the points of intersection of tangents to the circle at Q and Rdot
View SolutionIf the tangent at P (1, 1) on y2=x(2−x)2 meets the curve again at Q then the point Q is
View Solution
