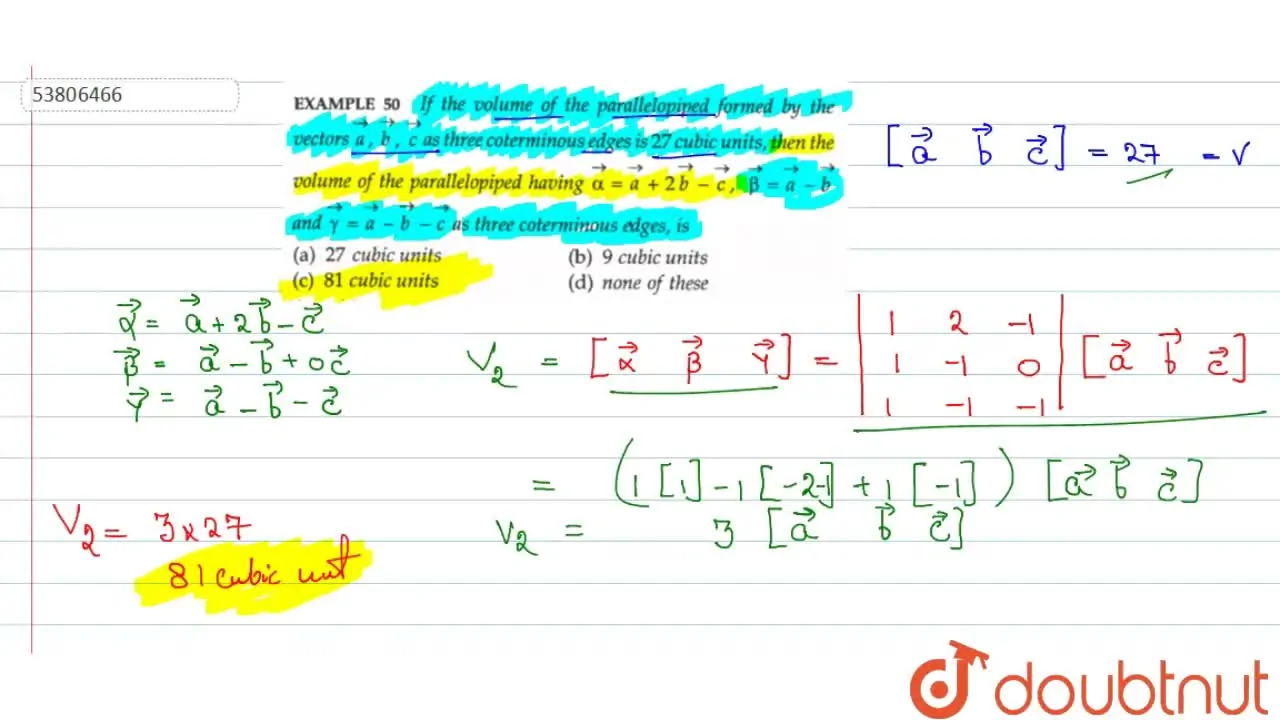
If the volume of the parallelopiped formed by the vectors →a,→b,→c as three coterminous edges is 27 units, then the volume of the parallelopiped having →α=→a+2→b−→c,→β=→a−→b
and →γ=→a−→b−→c as three coterminous edges, is
27 cubic units
9 cubic units
81 cubic units
none of these
The correct Answer is:C
We have ∣∣[→a→b→c]∣∣=27 cubic units
Now, [→α→β→γ]=∣∣
∣∣12−11−101−1−1∣∣
∣∣[→a→b→c]
⇒[→α→β→γ]=3[→a→b→c]
∴ Required volume =∣∣→α→β→γ∣∣
=3∣∣[→a→b→c]∣∣=3×27=81 cubic units
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Section II - Assertion Reason Type12videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test60videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALER AND VECTOR PRODUCTS OF TWO VECTORS EXERCISE - Section I - Solved Mcqs12videos
SCALER AND VECTOR PRODUCTS OF TWO VECTORS
Similar Questions
The volume of the tetrahedron formed by the coterminous edges →a,→b,→c is 3. Then the volume of the parallelopiped formed by the coterminous edges →a+→b,→b+→c,→c+→a is
View SolutionThe volume of a parallelopiped whose coterminous edges are 2→a,2→b,2→c , is
View SolutionIf V is the volume of the parallelopiped having three coterminous edges as →a,→b and →c, then the volume of the parallelopiped having three coterminous edges as
→α=(→a.→a)→a+(→a.→b)→b+(→a.→c)→c
→β=(→a.→b)→a+(→b.→b)→b+(→b.→c)→c
→γ=(→a.→c)→a+(→b.→c)→b+(→c.→c)→c isView SolutionThe volume of a tetrahedron fomed by the coterminus edges →a,→band→cis3 . Then the volume of the parallelepiped formed by the coterminus edges →a+→b,→b+→cand→c+→a is
View SolutionStatement 1: If V is the volume of a parallelopiped having three coterminous edges as →a,→b, and →c, then the volume of the parallelopiped having three coterminous edges as
→α=(→a.→a)→a+(→a.→b)→b+(→a.→c)→c
→β=(→a.→b)→a+(→b.→b)→b+(→b.→c)→c
→γ=(→a.→c)→a+(→b.→c)→b+(→c.→c)→c is V3
Statement 2: For any three vectors →a,→b,→c
∣∣ ∣ ∣∣→a.→a→a.→b→a.→c→b.→a→b.→b→b.→c→c.→a→c.→b→c.→c∣∣ ∣ ∣∣=[→a→b→c]3View SolutionIf |→a|=5,∣∣→b∣∣=3,|→c|=4 and →a is perpendicular to →b and →c such that angle between →b and →c is 5π6, then the volume of the parallelopiped having →a,→b and →c as three coterminous edges is
View SolutionIf V is the volume of the parallelepiped having three coterminous edges as →a,→b and →c, then the volume of the parallelepiped having three coterminous edges as
→α=(→a.→a)→a+(→a.→b)→b+(→a.→c)→c,
→β=(→b.→a)→a+(→b.→b)+(→b.→c)→c
and →λ=(→c.→a)→a+(→c.→b)→b+(→c.→c)→c isView SolutionStatement 1: Let V1 be the volume of a parallelopiped ABCDEF having →a,→b,→c as three coterminous edges and V2 be the volume of the parallelopiped PQRSTU having three coterminous edges as vectors whose magnitudes are equal to the areas of three adjacent faces of the parallelopiped ABCDEF. Then V2=2V21
Statement 2: For any three vectors →α,→β,→γ
[→α×→β,→β×→γ,→γ×→α]=[→α→β→γ]2View SolutionIf →a,→b,→c are vectors such that →a.→b=0 and →a+→b=→c then:
View SolutionIf [→a→b→c]=3, then the volume (in cubic units) of the parallelopiped with 2→a+→b,2→b+→c and 2→c+→a as coterminous edges is
View Solution