If θ is an angle in standard position and its terminal side passes thorugh the point (√32,−12) on the unit circle, then a possible value of θ is
7π6
4π3
5π3
11π6
The correct Answer is:D
To find the angle θ in standard position whose terminal side passes through the point (√32,−12) on the unit circle, we can follow these steps:
Step 1: Identify the coordinates
The point given is (√32,−12). Here, the x-coordinate is √32 and the y-coordinate is −12.
Step 2: Determine the quadrant
Since the x-coordinate is positive and the y-coordinate is negative, the point lies in the fourth quadrant.
Step 3: Use trigonometric identities
In the unit circle, we know that:
- cos(θ)=x
- sin(θ)=y
Thus, we have:
- cos(θ)=√32
- sin(θ)=−12
Step 4: Find the reference angle
The cosine value √32 corresponds to an angle of θ=π6 in the first quadrant.
Step 5: Determine the angle in the fourth quadrant
Since we are in the fourth quadrant, we can find θ using the formula:
θ=2π−reference angle
Substituting the reference angle:
θ=2π−π6
Step 6: Simplify the angle
To simplify:
θ=2π−π6=12π6−π6=11π6
Conclusion
Thus, a possible value of θ is:
θ=11π6
---
The point given is (√32,−12). Here, the x-coordinate is √32 and the y-coordinate is −12.
Since the x-coordinate is positive and the y-coordinate is negative, the point lies in the fourth quadrant.
In the unit circle, we know that:
- cos(θ)=x
- sin(θ)=y
- cos(θ)=√32
- sin(θ)=−12
The cosine value √32 corresponds to an angle of θ=π6 in the first quadrant.
Since we are in the fourth quadrant, we can find θ using the formula:
θ=2π−reference angle
Substituting the reference angle:
θ=2π−π6
To simplify:
θ=2π−π6=12π6−π6=11π6
Thus, a possible value of θ is:
θ=11π6
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In32videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE45videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE45videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST24videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE6videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
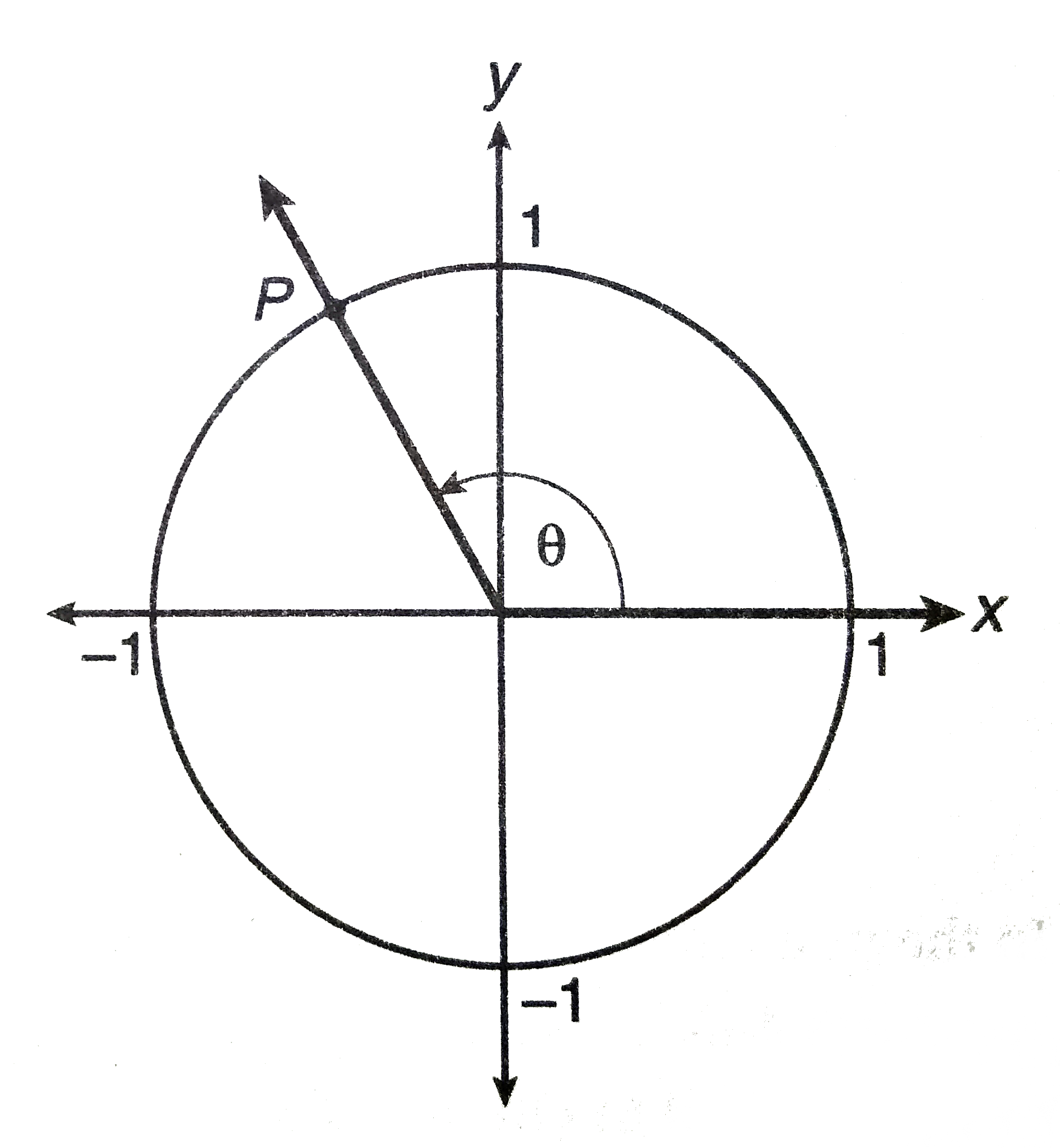
In the figure above, θ is an angle in standard position and its terminal side passes through the point P(−12,√32) on the unit circle. What is the possible value of θ?A23πB56πC76πD43π - Question 2 - Select One
If P(−3,4) is a point on the terminal side of angle θ, what is the value of cosθ?
A−34B−35C34D45
Find the general value of θ
sinθ=√32View SolutionIf π2<θ<π, then possible answers of √2+√2+2cos4θ is/are :
View SolutionIf θ is an acute angle and sinθ=cosθ , find the value of 2tan2θ+sin2θ−1
View SolutionIf the points (−2,0),(−1,1√3) and (cosθ,sinθ) are collinear, then the number of value of θ∈[0,2π] is
View SolutionA circle touches the hypotenuse of a right angled triangle at its middle point and passes through the mid-point of the shorter side. If aandb(a<b) be the lengths of the sides, then prove that the radius of the circle is b4a√a2+b2
View Solution(i) Find the equation of line passing through (2,2) and makes an angle of 135∘ from positive direction of X-axis.
(ii) Find the equation of a line passing through the point (2,1) and makes an angle 'θ' from the positive direction of X-axis where cosθ=−13.View Solution

