If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
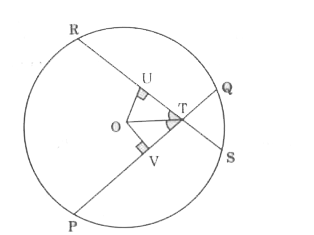 Solution in Kannada
Solution in Kannada
Step by step video & image solution for If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.57videos
CIRCLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.64videos
CIRCLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.33videos
CIRCLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 11.48videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - EXERCISE 9.21videos
CO-ORDINATE GEOMETRY
Similar Questions
In the given figure, A, B and C are three points on a circle with centre O such that ∠BOC=30∘and∠AOB=60∘. If D is a point on the circle other than the arc ABC, find ∠ADC.
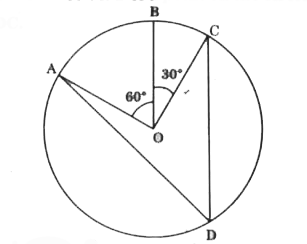 04:09View Solution
04:09View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
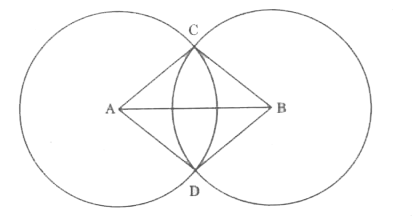 04:55View Solution
04:55View SolutionDraw different pairs of circles. How many points does each pair have in common ? What is the maximum number of common points ?
04:55View SolutionParallelogram ABCD and rectangle ABEF are on the base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
02:11View SolutionSee fig and Write the following :
(i) The coordinates of B
(ii) The coordinates of C
(iii) The point identified by the coordinates (-3,-5)
(iv) The point identified by the coordinates (2,-4)
(v) The abscissa of the point D .
(vi) The ordinates of the point H .
(vii) The co-ordinates of the point L .
(viii) The co-ordinates of the point M .
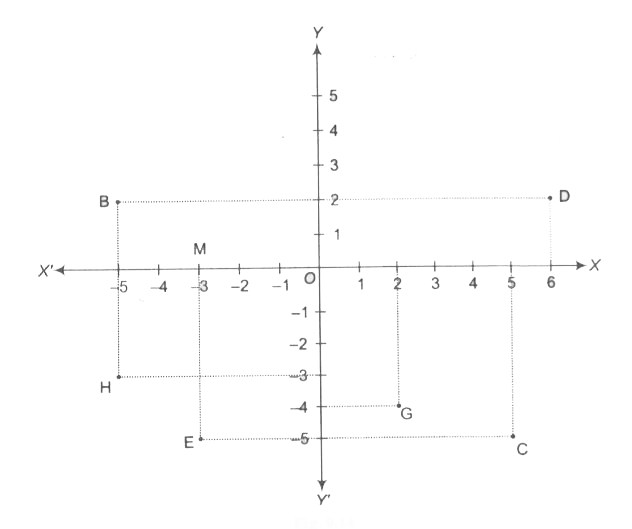 02:45View Solution
02:45View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
02:17View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
05:41View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
02:10View SolutionDetermine the point of symmetry of a regular hexagon.
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:18View Solution
02:18View SolutionMatch the following Column A to Column B
 View Solution
View SolutionThe inequation represented by the graph given below is :
04:38View SolutionThe inequation that best describes the graph given below is _________
06:53View SolutionThe inequation that best describes the following graph is _________
08:19View Solution

