If two natural numbers r and s are drawn one at a time, without replacement from the set S={1,2,3,….n}, then find P(r≤p/s≤p) where p∈S.
To solve the problem, we need to find the probability P(r≤p≤s) where p is a natural number drawn from the set S={1,2,3,…,n} and r and s are also drawn from the same set without replacement.
1. Understanding the Set:
The set S contains n natural numbers: S={1,2,3,…,n}.
2. Choosing Numbers:
We draw two numbers r and s from the set S without replacement. This means once we draw a number, it cannot be drawn again.
3. Identifying the Range:
We want to find the probability that a number p drawn from S satisfies the condition r≤p≤s.
4. Calculating the Total Outcomes:
The total number of ways to choose 2 numbers from S is given by (n2), which is equal to n(n−1)2.
5. Calculating Favorable Outcomes:
For the chosen numbers r and s, we can assume without loss of generality that r<s. The numbers p that satisfy r≤p≤s are the integers from r to s, inclusive. The count of such integers is s−r+1.
6. Finding the Probability:
The probability P(r≤p≤s) can be calculated as the ratio of the number of favorable outcomes to the total outcomes:
P(r≤p≤s)=s−r+1n
7. Final Expression:
Thus, the final probability can be expressed as:
P(r≤p≤s)=s−r+1n
Conclusion:
The probability that a number p drawn from the set S satisfies r≤p≤s is given by s−r+1n.
The set S contains n natural numbers: S={1,2,3,…,n}.
We draw two numbers r and s from the set S without replacement. This means once we draw a number, it cannot be drawn again.
We want to find the probability that a number p drawn from S satisfies the condition r≤p≤s.
The total number of ways to choose 2 numbers from S is given by (n2), which is equal to n(n−1)2.
For the chosen numbers r and s, we can assume without loss of generality that r<s. The numbers p that satisfy r≤p≤s are the integers from r to s, inclusive. The count of such integers is s−r+1.
The probability P(r≤p≤s) can be calculated as the ratio of the number of favorable outcomes to the total outcomes:
P(r≤p≤s)=s−r+1n
Thus, the final probability can be expressed as:
P(r≤p≤s)=s−r+1n
The probability that a number p drawn from the set S satisfies r≤p≤s is given by s−r+1n.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions15videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions38videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example101videos
MATRICES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers15videos
RELATIONS AND FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the probability that the sum of two different numbers randomly picked (without replacement) from the set S={1,2,3,4} is 5 ?
A1/5B3/16C1/4D1/3 - Question 2 - Select One
Which one of the following numbers can be removed from the set S={0,2,4,5,9} without changing the average of set S?
A0B2C4D5
Two numbers are selected randomly from the set S={1,2,3,4,5,6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is (a) 115 (b) 1415 (c) 15 (d) 45
View SolutionTwo numbers are selected randomly from the set S={1,2,3,4,5,6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is (a) 115 (b) 1415 (c) 15 (d) 45
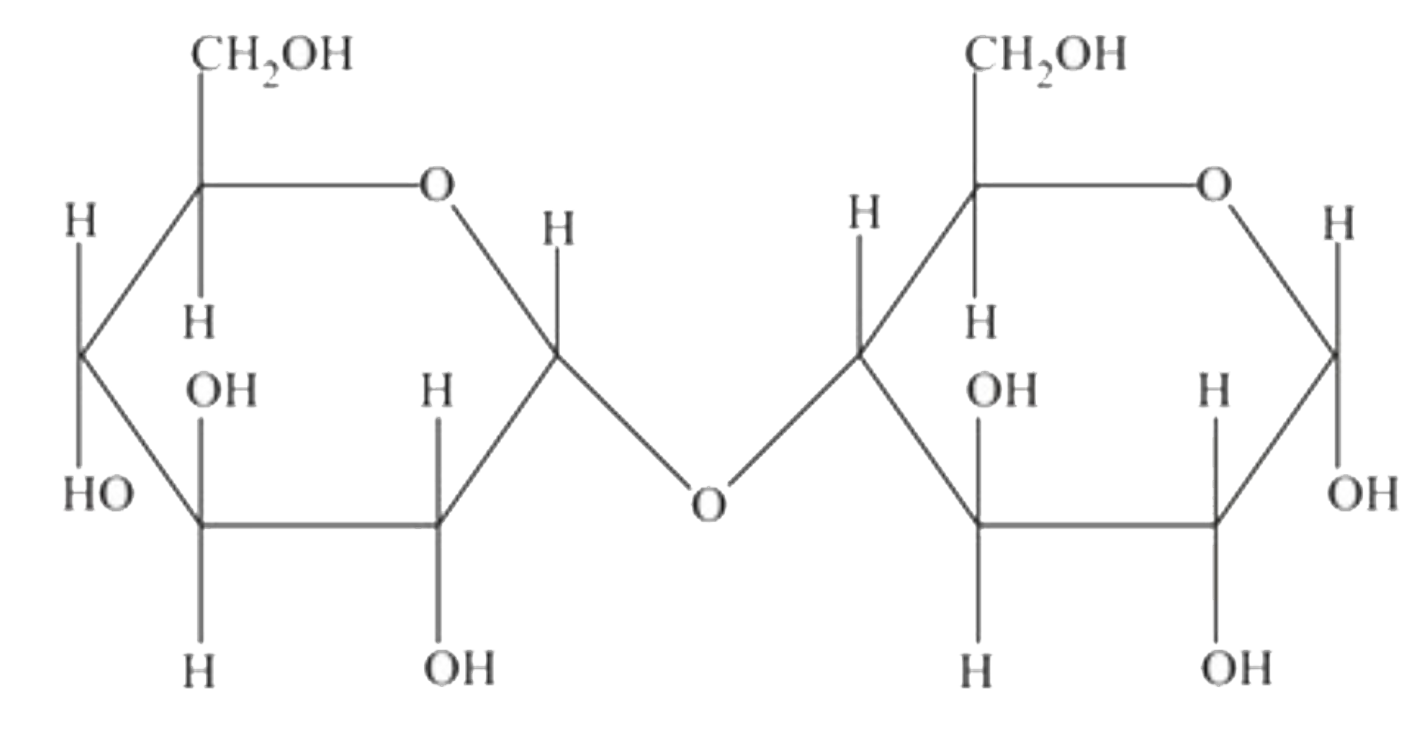
View SolutionIf number of aldose, ketose, furanose and pyranose units present in maitose are p, q, r, s respectively. Find the value of p+q+r+s
 View Solution
View Solutionlet Sn denote the sum of the cubes of the first n natural numbers and sn denote the sum of the first n natural numbers , then n∑r=1Srsr equals to
View Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-View SolutionThere are two sets A and B each of which consists of three numbers in GP whose product is 64 and R and r are the common ratios such that R=r+2. If pq=32, where p and q are sum of numbers taken two at a time respectively in the two sets.
The value of p isView Solution

