If two parallel lines are cut by a transversal, then the alternate interior angles are equal
TRUE
FALSE
Cannot be determined
None of these
The correct Answer is:A
To demonstrate that if two parallel lines are cut by a transversal, then the alternate interior angles are equal, we can follow these steps:
1. Draw Two Parallel Lines:
- Start by drawing two straight lines that are parallel to each other. Let's label them as line L and line M.
2. Draw a Transversal:
- Next, draw a third line that intersects both parallel lines. This line will be called the transversal, and we can label it as line N.
3. Identify Alternate Interior Angles:
- When the transversal intersects the parallel lines, it creates several angles. Identify two pairs of alternate interior angles.
- For example, let’s label one pair as angle A and angle B, which are located on opposite sides of the transversal but inside the parallel lines.
- Similarly, label another pair of alternate interior angles as angle C and angle D.
4. State the Relationship:
- According to the properties of parallel lines cut by a transversal, we state that angle A is equal to angle B (∠A = ∠B) and angle C is equal to angle D (∠C = ∠D).
5. Conclusion:
- Therefore, we conclude that if two parallel lines are cut by a transversal, then the alternate interior angles are equal.
- Start by drawing two straight lines that are parallel to each other. Let's label them as line L and line M.
- Next, draw a third line that intersects both parallel lines. This line will be called the transversal, and we can label it as line N.
- When the transversal intersects the parallel lines, it creates several angles. Identify two pairs of alternate interior angles.
- For example, let’s label one pair as angle A and angle B, which are located on opposite sides of the transversal but inside the parallel lines.
- Similarly, label another pair of alternate interior angles as angle C and angle D.
- According to the properties of parallel lines cut by a transversal, we state that angle A is equal to angle B (∠A = ∠B) and angle C is equal to angle D (∠C = ∠D).
- Therefore, we conclude that if two parallel lines are cut by a transversal, then the alternate interior angles are equal.
Topper's Solved these Questions
Similar Questions
Which of the following statements are true (T) and which are false (F)? Give reasons. (i)If two lines are intersected by a transversal, then corresponding angles are equal. (ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal. (iii)Two lines perpendicular to the same line are perpendicular to each other. (iv)Two lines parallel to the same line are parallel to each other. (v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.
View SolutionIf two parallel lines intersected by a transversal , then name the pair of angles formed that are equal .
View Solution
Knowledge Check
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryIf two parallel lines are cut by two distinct transversals, then the quadrilateral formed by these four lines will always be a:
AparallelogramBrhombusCsquareDtrapeziumQuestion Stimulus :-
In the given diagram two parallel lines are cut by a transversal, find the measure of angle 4, if angle 7 = 20∘
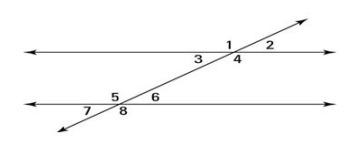 A170∘B160∘C20∘D180∘
A170∘B160∘C20∘D180∘
If two parallel lines are cut by two distinct transversals, then the quadrilateral formed by the four lines is always a :
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionRead the following statements which are taken as axioms
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent ? Justify your answer.
View SolutionAngles made by a transversal with two lines - interior angles.
View SolutionIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
View Solution
