If two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.

Video Solution

Text Solution

Verified by Experts

Given : AB||CD and l cuts them
Aslo EF, GF, EH and GH are bisectors of $∠ A E G, ∠ E G C, ∠ E G D$ respectively,
$i . e ., ∠ 1 = ∠ 2, ∠ 3 = ∠ 4, ∠ 5 = ∠ 6 and ∠ 7 = ∠ 8$
To Prove EFGH is a rrectangle
Proof : Since AB|| CD and l cuts them,
$∴ ∠ 1 + ∠ 2 = ∠ 5 + ∠ 6$
(all $∠$ formed with AB, CD and l i.e., 3 necessary line)

$\Rightarrow ∠ 2 + ∠ 2 = ∠ + 5 + ∠ 5 (∴ ∠ 1 = ∠ 2 and ∠ 5 = ∠ 6)$
$\Rightarrow 2 ∠ 2 = 2 ∠ 5$
$\Rightarrow ∠ 2 = ∠ 5$
But these are the alternate angles formed with 3 necesaary lines EF, GH and l
$∴ E F ∣ ∣ G H ... . . (1)$
Similarly, we can prove that $F G ∣ ∣ G H ... . . (2)$
$∴$ From eqs. (1) and (2), we get
EFGH is a parallelogram (pairs of apposite sides are parallel)....(3)
Now, $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 180^{\circ} (L . P . A .)$
$\Rightarrow ∠ 2 + ∠ 2 + ∠ 3 + ∠ 3 = 180^{\circ} (∴ ∠ 1 = ∠ 2 and ∠ 3 = ∠ 4$ , as EF and EH are angle bisectors)
$∴ 2 ∠ 2 + 2 ∠ 3 = 180^{\circ}$
$\Rightarrow ∠ 2 + ∠ 3 = 90^{\circ} ... . . (4)$
So, from eqs. (3) and (4) we can say that
EFGH is a reactangle. ( $∴$ parallelogram has one right agnle)

If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
Aequal
Badjacent
CSupplementary
DComplementary
If two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
A1
B2
C3
D4
Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a

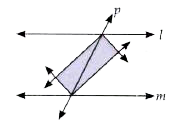ATrapezium
BKite
CParallelogram
DSquare