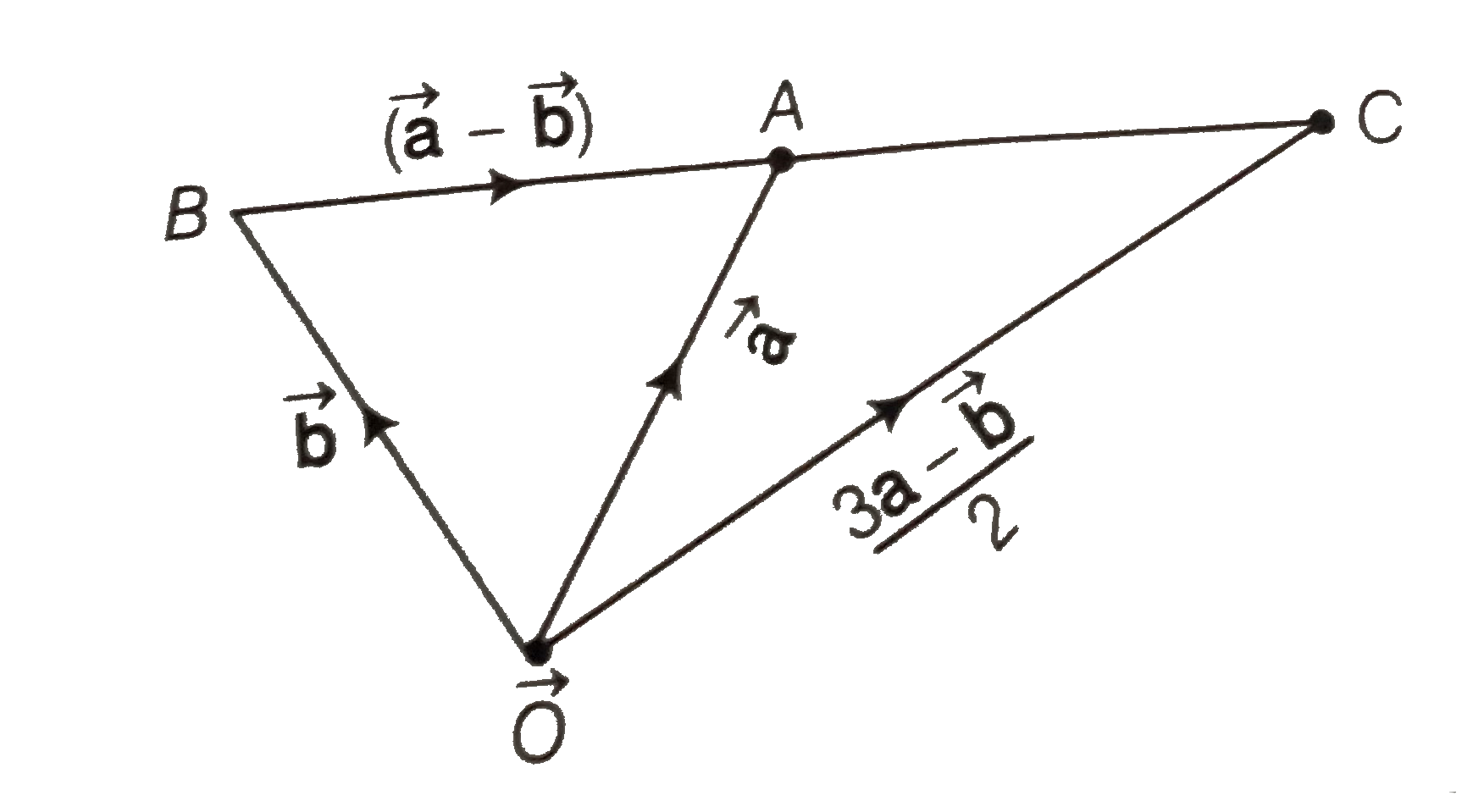
If →aand→b are position vectors of AandB respectively, find the position vector of a point ConBA produced such that BC=1.5BA.
Since, −−→AO=→aand−−→OB=→b
∴−−→BA=−−→OA−−−→OB=→a−→b
and 1.5−−→BA=1.5(→a−→b)
Since−−→BC=1.5−−→BA=1.5(→a−→b)
−−→OC−−−→OB=1.5→a−1.5→b
−−→OC=1.5→a−1.5→b+→b [:.vec(OB)=vecb]
=1.5→a−0.5→b
=3→a−→b2
Graphically, explanation of the above solution is given below
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - OBJECTIVE TPYE QUESTIONS
27 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
16 Videos
Similar Questions
If →a,→b are the position vectors of A,B respectively, find the position vector of a point C in AB produced such that AC=3AB and that a point D in BA produced such that BD=2BA .
View SolutionIf →a,→b are the position vectors of A,B respectively, find the position vector of a point C in AB produced such that AC=3AB and that a point D in BA produced such that BD=2BA .
View SolutionIf a and b are position vectors of A and B respectively the position vector of a point C on AB produced such that −−→AC=3−−→AB is
View SolutionIf →a and →b are position vectors of A and B respectively, then the position vector of a point C in −−→AB produced such that −−→AC =2015 −−→AB is
View SolutionIf →aand→b are position vectors of points AandB respectively, then find the position vector of points of trisection of AB .
View SolutionLet ABCD be as parallelogram. If →a, →b, →c be the position vectors of A, B, C respectively with reference to the origin O, find the position vector of D reference to O.
View SolutionIf →a, →b, →c are position vectors o the point A, B, and C respectively, write the value of →AB+→BC+→AC.
View Solution→AB=3ˆi−ˆj+ˆkand→CD=−3ˆi+2ˆj+4ˆk are two vectors. The position vectors of the points AandC are =6ˆi+7ˆj+4ˆkand=−9ˆj+2ˆk respectively. Find the position vector of a point P on the line AB and a point Q on the line CD such that →PQ is perpendicular to →ABand→CB both.
View SolutionIf →aand→b are two vectors of magnitude 1 inclined at 1200 , then find the angle between →band→b−→a.
View SolutionIf →a, →b, →c are position vectors of the vertices A, B and C respectively, of a triangle ABC, write the value of →AB+→BC+→CA.
View Solution
