If →a=(1,−1,−6),→b=(1,−3,4)and→c=(2,−5,3), then compute the following (i) →a.(→b×→c), (ii) →a×(→b×→c)
(iii) (→a×→b)×→c.Solution in Telugu
The correct Answer is:(i) 0
(ii) 29 (iii) −40→i+62→j+130→k
Step by step video, text & image solution for If veca=(1,-1,-6),vecb=(1,-3,4) and vec(c)=(2,-5,3), then compute the following (i) veca.(vecbxxvec(c)), (ii) vecaxx(vecbxxvec(c)) (iii) (vecaxxvecb)xxvec(c). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - PRODUCT OF VECTORSEXERCISE - EXERCISE 5(c) II
17 Videos
- PRODUCT OF VECTORSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - PRODUCT OF VECTORSEXERCISE - EXERCISE 5(c) III
11 Videos
- PRODUCT OF VECTORSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - PRODUCT OF VECTORSEXERCISE - EXERCISE 5(b) III
8 Videos
- PAIR OF STRAIGHT LINES BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - PAIR OF STRAIGHT LINES EXERCISE - EXERCISE - 4(c) III.
3 Videos
- PROPERTIES OF TRIANGLESBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - PROPERTIES OF TRIANGLESEXERCISE - TEXTUAL EXERCISES ( EXERCISE - 10(b) ) III.
11 Videos
Similar Questions
If [→b →c →d]+[→c →a →d]+[→a →b →d]=[a b c] then show that the points with position vectors a,b,c and →d are coplanar.
View SolutionIf A=(1, -2, -1), B= (4, 0, -3), C = (1, 2, -1), D=(2, -4, -5), then distance between AB and CD is
View SolutionIf ¯a,¯b,¯c respresents the vertices A, B, and C respectively of ΔABC then prove that ∣∣(¯aׯb)+(¯bׯc)+(¯cׯa)∣∣ is twice the area of ΔABC.
View SolutionFind the condition for the chord lx + my=1 of the circle x2+y2=a2 to subtend a right angle at the origin.
View SolutionIn ΔABC Prove that
cosA+cosB+cosC=1+rR
View SolutionShow that if →A.(→B×→c)=0, then →A,→B and →c are coplanar .
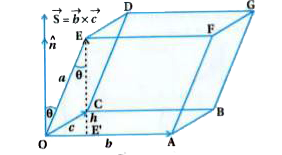
View SolutionShow that →a.(→b×→c) is equal in magnitude to the volume of the parallelpiped formed by the vectors →a,→band→c
View Solutionयदि →a=2ˆi−3ˆj+ˆk, →b=ˆi−ˆj+2ˆk और →c=2ˆi+ˆj−ˆk हो, तो →a×(→b×→c) का मान ज्ञात कीजिए |
View SolutionShow that veca.(vecbxxvec c) is equal in magnitude to the volume of the parallelpiped formed by the vectors veca,vecb and vec c
View SolutionShow that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors, →a,→band→c
View SolutionCompute →a×(→b+→c)+→b×(→c+→a)+→c×(→a+→b).
View SolutionIf veca+vecb+vec(c)=vec0 , then prove that vecaxxvecb=vecbxxvec(c)=vec(c)xxveca .
View SolutionIf ¯a,¯b,¯c respresents the vertices A, B, and C respectively of ΔABC then prove that ∣∣(¯aׯb)+(¯bׯc)+(¯cׯa)∣∣ is twice the area of ΔABC.
View SolutionIf →a=2→i+3→j+4→k,→b=→i+→j−→kand→c=→i−→j+→k, then compute →a×(→b×→c) and verify that it is perpendicular to →a.
View SolutionIf →a=→i−2→j−3→k,→b=2→i+→j−→k,→c=i+3→j−2→k, then compute →a. (→b×→c).
View Solution
