If x=1+logtt2, y=3+2logtt, find dydx .
A
1t
B
−1
C
1
D
t
Video Solution
Text Solution
The correct Answer is:D
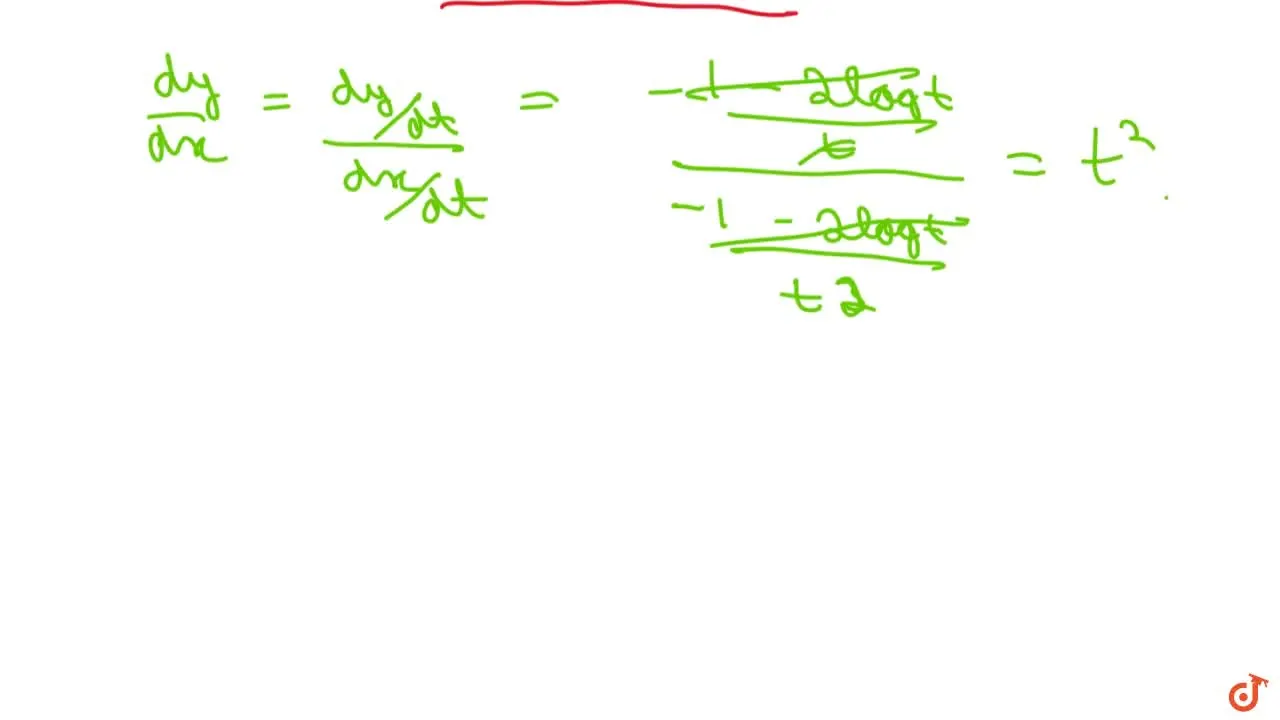
Given that , x=1+lottt2 and y=3+2logtt
On differentiating both functions w.r.t.t, we get
dxdt=t2.1t−(1+logt)2tt4
and dydt=1.2t−(3+2logt)×1t2
⇒dxdt=t−2t−2tlogtt4 and dydt=2−3−2logtt2
⇒dxdt=−1+2logtt3 and dydt=−1+2logtt2
∴dydx=dydt.dtdx=−1+2logtt2×t3(1+2logt)
⇒dydx=t
|
Updated on:21/07/2023
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - DIFFERENTIATION EXERCISE - EXERCISE 1 (HIGHER ORDER DERIVATIVE )15videos
DIFFERENTIATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - DIFFERENTIATION EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS)80videos
DIFFERENTIATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - DIFFERENTIATION EXERCISE - EXERCISE 1 (LOGARITHMIC DIFFERENTIATION )17videos
DIFFERENTIATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - DIFFERENTIAL EQUATIONEXERCISE - MHT CET Corner27videos
DIFFERENTIAL EQUATION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FACTORIZATION FORMULAE EXERCISE - EXERCISE 221videos
FACTORIZATION FORMULAE
Similar Questions
If x=1+logtt2, y=3+2logtt, find dydx .
View SolutionIf x=1+logtt2,y=3+2logtt,f i n ddydx.
View SolutionIf x=1+logtt2 and y=3+2logtt, then dy/dx is equal to
View SolutionIf x=1+logtt2,y=3+2logtt,t>0, prove that :
dydx=tView SolutionIf sinx=2t1+t2 , tany=2t1−t2 , find dydx .
View SolutionIf x=a(1+t21−t2) and y=2t1−t2 , find dydx
View SolutionIf x=a(1+t21−t2)andy=2t1−t2,f i n ddydx
View SolutionIf x=1+logtt2,y=3+2logtt,t>0, prove that :
ydydx−2x(dydx)2=1.View SolutionIf sinx=2t1+t2,tany=2t1−t2,f i n ddydx.
View SolutionIf x=1−t21+t2 and y=2at1+t2, then dydx=
View Solution