If X and Y are two events such that PX/Y)=12,P(Y/X)=13 and P(X∩Y)16. Then, which of the following is/are correct ?
P(X∪Y)=23
X and Y are independent
X and Y are not independent
P(Xc∩Y)=13
The correct Answer is:A, B
To solve the problem, we need to find the probabilities of events X and Y based on the given conditions. Let's break down the steps systematically.
Step 1: Write down the given probabilities
We have the following probabilities:
1. P(X|Y)=12
2. P(Y|X)=13
3. P(X∩Y)=16
Step 2: Use the definition of conditional probability
The conditional probability P(X|Y) can be expressed as:
P(X|Y)=P(X∩Y)P(Y)
Substituting the known values:
12=16P(Y)
Step 3: Solve for P(Y)
Cross-multiplying gives:
P(Y)=16×2=13
Step 4: Use the definition of the other conditional probability
Now we can use P(Y|X):
P(Y|X)=P(X∩Y)P(X)
Substituting the known values:
13=16P(X)
Step 5: Solve for P(X)
Cross-multiplying gives:
P(X)=16×3=12
Step 6: Verify the union of probabilities
We can use the formula for the union of two events:
P(X∪Y)=P(X)+P(Y)−P(X∩Y)
Substituting the values we found:
P(X∪Y)=12+13−16
Step 7: Find a common denominator and calculate
The common denominator for 2, 3, and 6 is 6:
P(X∪Y)=36+26−16=46=23
Step 8: Conclusion
We have determined:
- P(X)=12
- P(Y)=13
- P(X∩Y)=16
- P(X∪Y)=23
Based on these calculations, we can conclude that options A and B are correct.
We have the following probabilities:
1. P(X|Y)=12
2. P(Y|X)=13
3. P(X∩Y)=16
The conditional probability P(X|Y) can be expressed as:
P(X|Y)=P(X∩Y)P(Y)
Substituting the known values:
12=16P(Y)
Cross-multiplying gives:
P(Y)=16×2=13
Now we can use P(Y|X):
P(Y|X)=P(X∩Y)P(X)
Substituting the known values:
13=16P(X)
Cross-multiplying gives:
P(X)=16×3=12
We can use the formula for the union of two events:
P(X∪Y)=P(X)+P(Y)−P(X∩Y)
Substituting the values we found:
P(X∪Y)=12+13−16
The common denominator for 2, 3, and 6 is 6:
P(X∪Y)=36+26−16=46=23
We have determined:
- P(X)=12
- P(Y)=13
- P(X∩Y)=16
- P(X∪Y)=23
Topper's Solved these Questions
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Subjective Type Questions)
15 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
28 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
Similar Questions
Knowledge Check
If p(x)=|2−x|+12, which of the following could be the graph of y=p(x) ?
A B
B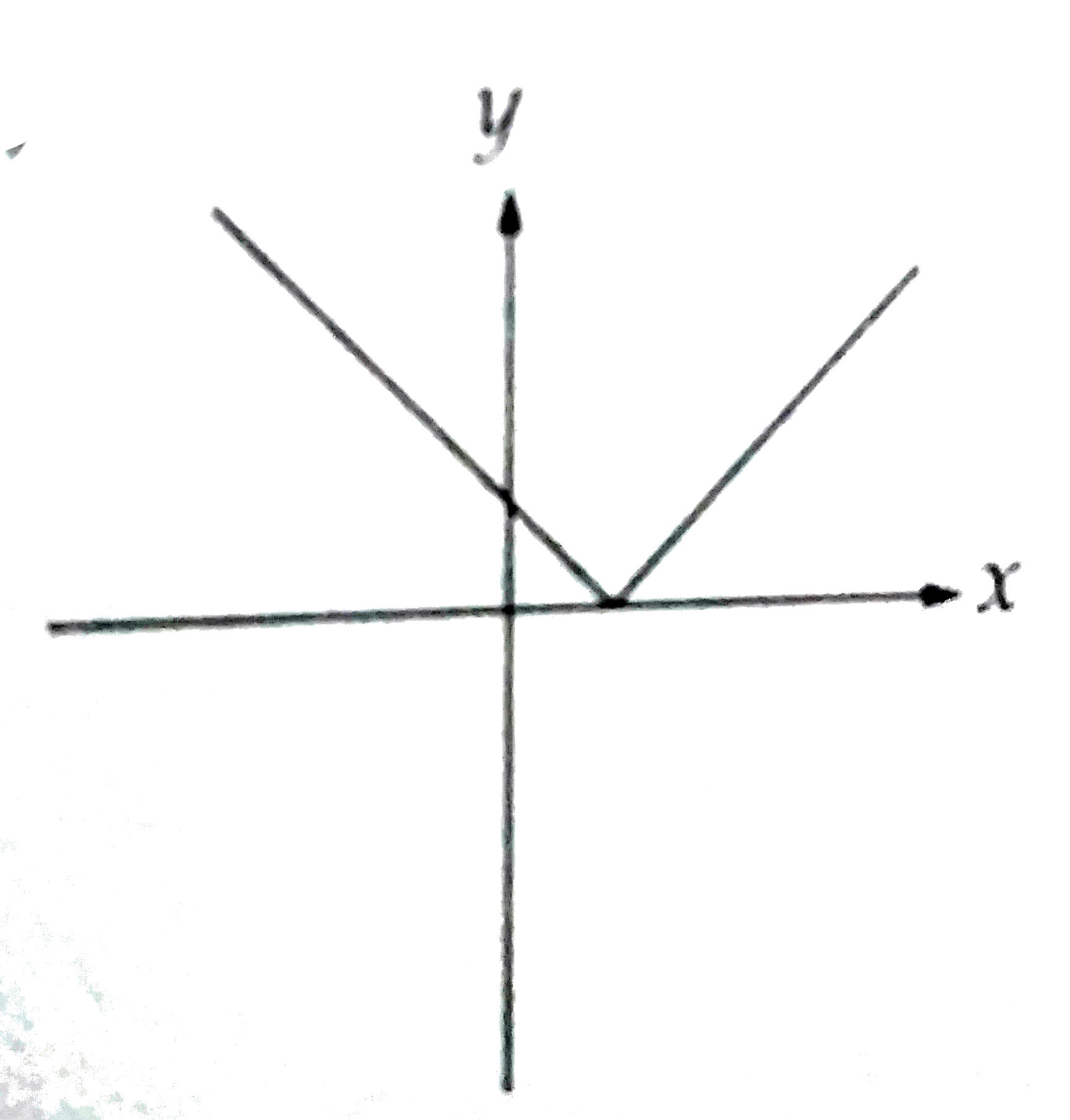 C
C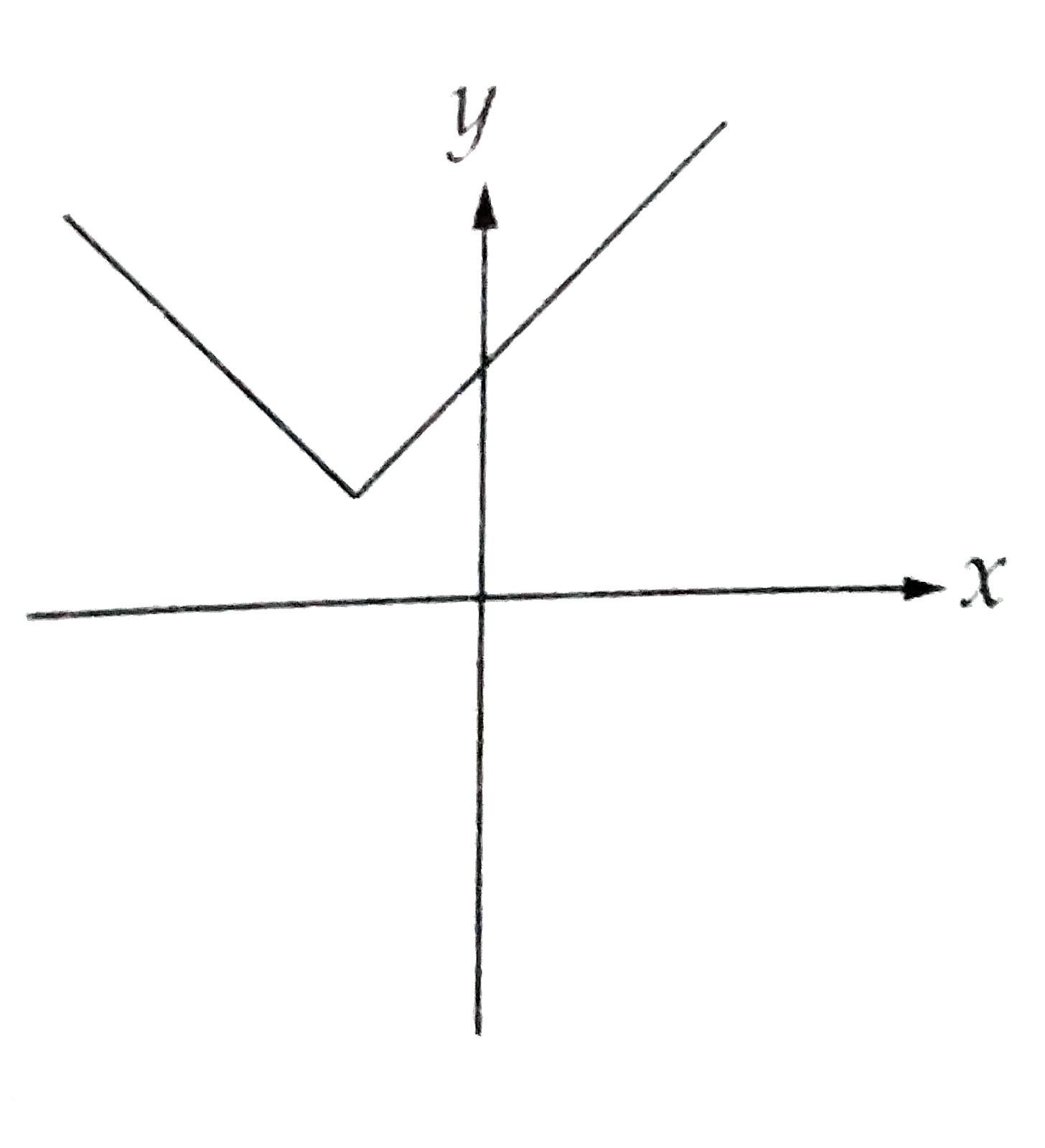 D
D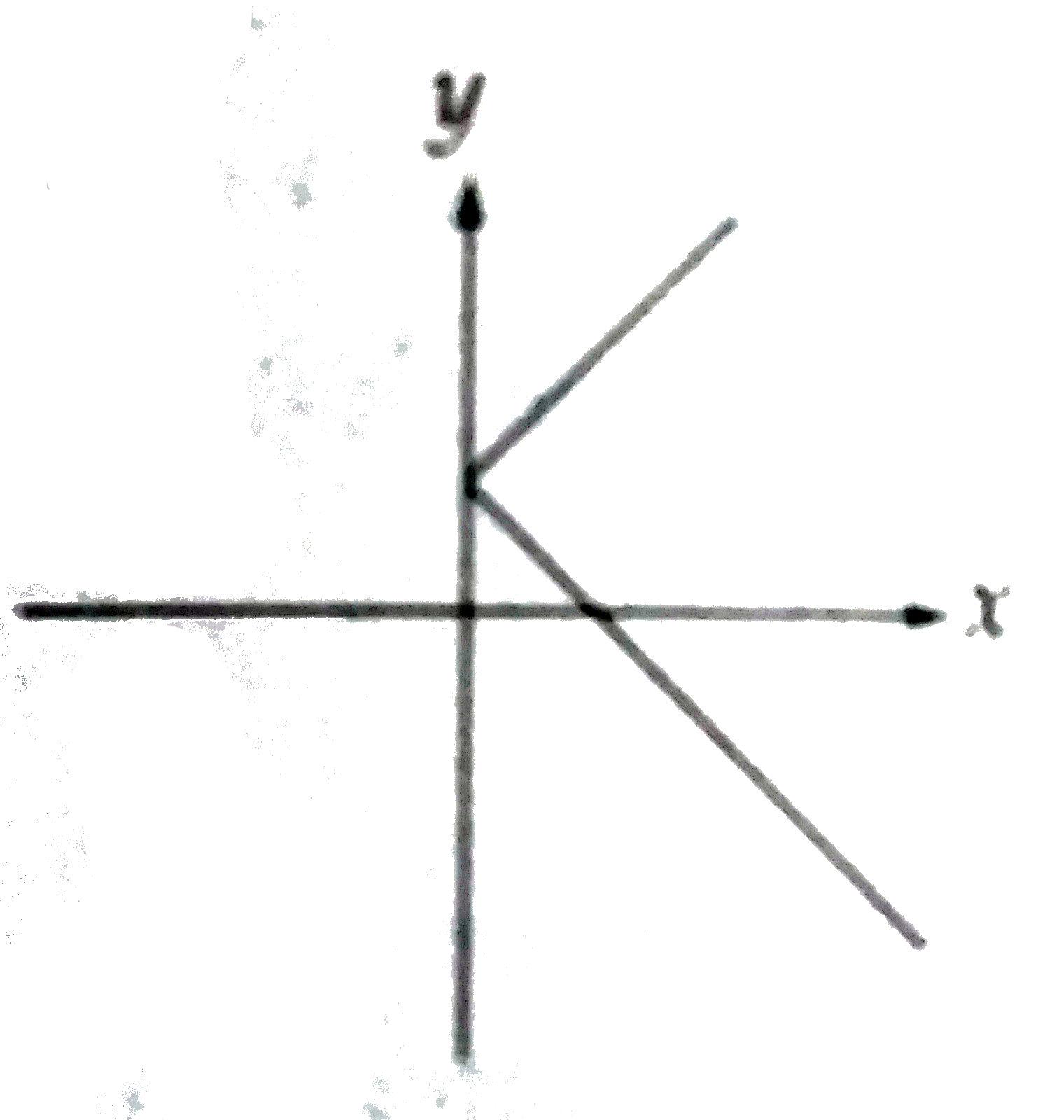
If P(X)=310,P(Y)=25andP(X∪Y)=35,then P(YX)+P(XY) equals
A14B13C512D712
If x,y,z, are in A.P. and x2,y2,z2 are in H.P., then
which of the following is correct ?
View SolutionFor any two positive integers x and y f(x,y)=1(x+1)!+1(x+2)!+1(x+3)!+……..+1(x+y)!, then which of the following options is/are correct
View SolutionLet P1:2x+y−z=3 and P2:x+2y+z=2 be two planes. Then, which of the following statement(s) is (are) TRUE?
View Solutionx+y=2 and x−y=2 are tangents on a parabola at (1,1) and (4,2) respectivley. Which of the followings is/are correct.
View SolutionFind the value of x and y
12x+13y=2
13x+12y=136
View SolutionTangents are drawn from the point P(1,−1) to the circle x2+y2−4x−6y−3=0 with centre C, A and B are the points of contact. Which of the following are correct?
View Solution
