If x is a positive acute angle and cosx=a, an expression for tanx in terms of a is
1−aa
√1−a2
√1−a2a
11−a
The correct Answer is:C
To find an expression for tanx in terms of a given that cosx=a and x is a positive acute angle, we can follow these steps:
Step 1: Use the Pythagorean Identity
We know from trigonometric identities that:
sin2x+cos2x=1
Since we are given cosx=a, we can substitute a into the identity:
sin2x+a2=1
Step 2: Solve for sin2x
Rearranging the equation gives us:
sin2x=1−a2
Step 3: Take the Square Root
To find sinx, we take the square root of both sides:
sinx=√1−a2
Since x is a positive acute angle, sinx is positive, so we only consider the positive root.
Step 4: Use the Definition of tanx
We know that:
tanx=sinxcosx
Substituting the values we have:
tanx=√1−a2a
Final Expression
Thus, the expression for tanx in terms of a is:
tanx=√1−a2a
---
We know from trigonometric identities that:
sin2x+cos2x=1
Since we are given cosx=a, we can substitute a into the identity:
sin2x+a2=1
Rearranging the equation gives us:
sin2x=1−a2
To find sinx, we take the square root of both sides:
sinx=√1−a2
Since x is a positive acute angle, sinx is positive, so we only consider the positive root.
We know that:
tanx=sinxcosx
Substituting the values we have:
tanx=√1−a2a
Thus, the expression for tanx in terms of a is:
tanx=√1−a2a
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
Knowledge Check
If x is an acute angle, which expressions is not equivalent to cosx?
A−cos(−x)Bsin(π2−x)C−cos(2+π)Dcos(x−2π)Angle x is one of the acute angles in a right triangle. If the measure of angles is 30∘, what is the value of (sinx)2+(cosx)2 ?
A14B12C1D2
Show, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View SolutionIf x,y,z be all positive acute angles then the least value of tanx(coty+cotz)+tany(cotz+cotx)+tanz(cotx+coty) is
View SolutionA positive acute angle is divided into two parts whose tangents are 12and13. Show that the angle is π4.
View Solution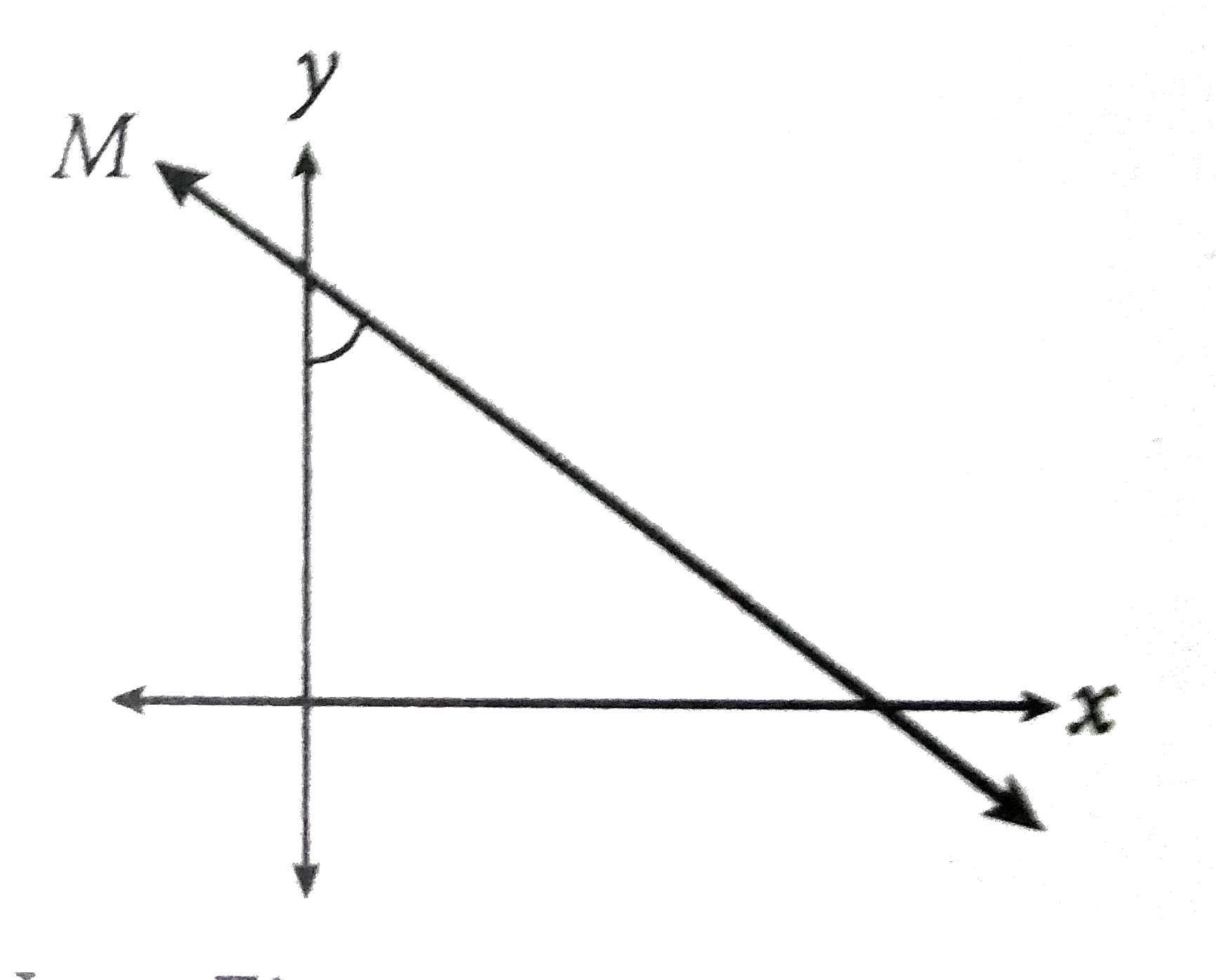
The equation of line M shown above is y=−34x+5. Given that angle A is the acute angle formed by the intersection of line M and the y-axis, which expression could be used to find the measure of angle A?
View SolutionProve the following identity, where the angles involved are acute angles for which the expressions are defined.
cosA1+sinA+1+sinAcosA=2secA
View SolutionProve the following identity, where the angles involved are acute angles for which the expressions are defined.
(i) (cosecθ−cotθ)2=1−cosθ1+cosθ
View Solution
