If X is the random varibale with distribution function F(x) given by
F(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩0−∞<x<032(x−x33)0≤x<113≤x<∞
Find P(0.3<x<0.5) Solution in Tamil
Step by step video & image solution for If X is the random varibale with distribution function F(x) given by F(x)={{:(0,-inftyltxlt0),(3/2(x-(x^(3))/(3)),0lexlt1),(1,3lexltinfty):} Find P(0.3 lt x lt 0.5) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.15videos
PROBABILITY DISTRIBUTIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.218videos
PROBABILITY DISTRIBUTIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - PROBLEMS FOR PRACTICE (ANSWER THE FOLLOWING QUESTIONS )22videos
ORDINARY DIFFERENTIAL EQUATIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - THEORY OF EQUATIONSEXERCISE - Problems for practice (Answer the following)21videos
THEORY OF EQUATIONS
Similar Questions
Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its inverse images.
02:52View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
02:14View SolutionFind the order and degree of the following differential equation
y''=(2+y')3402:40View SolutionIf α and β are the roots of 2x2−5x+3=0 form the equation whose roots are α2 and β2
05:37View SolutionIf p.d.f, of continuous random variable X is f(x) = {(2x^3,;0 lt= x lt=1), (0,;" otherwise"):}. Find P (X lt= 0.5) and P (0.5 lt= X lt= 1)
03:53View SolutionThe p.d.f of a random variable X is given by f(x)=3(1−2x2),0<x<1
= 0 , otherwise
Find P(14<X<13)05:58View SolutionIf the function f(x)=x23,−1<x<2
= 0 , otherwise is a p.d.f of X, then P(X<0) is06:44View SolutionThe p.d.f of continuous random variable X is given by f(x)=x8,0<x<4=0 otherwise. Find (i) P(X<2)(ii)P(2<X≤3)(iii)P(X>3.)
04:09View SolutionGiven the probability density functio (p.d.f) of a continuos random variable X as. f(x)=x23,−1<x<2
Determine the cumulative distribution function (c.d.f) X and hence find P(X<1),P(X>0),P(1<X<2).10:47View SolutionThe cumculative distribution function of a discrete random variable is given by
F(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0−∞<x<−10.15−1≤x<00.350≤x<10.601≤x<20.852≤x<313≤x<∞
Find (i) the probability mass function (ii) P(X<1) and (iii) P(X≥2).01:17View SolutionThe cumculative distribution function of a discrete random variable is given by
F(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0for −∞<x<012for 0≤x<135for 1≤x<245for 2≤x<3910for 3≤x<41for 4≤x<∞
Find (i) the probability mass function (ii) P(X<3) and (iii) P(X≥2).03:56View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.5≤X<1.5)02:55View SolutionIf X is the random variable with probability density function f(x) is given by
f(x)=⎧⎪⎨⎪⎩x+1−1≤x<0−x+10≤x<10otherwise
then find (i) the distribution function F(x) (ii) P(−0.5≤X≤0.5)07:29View SolutionIf the p.m (probability mass function ) f(x) of a random varibale X is
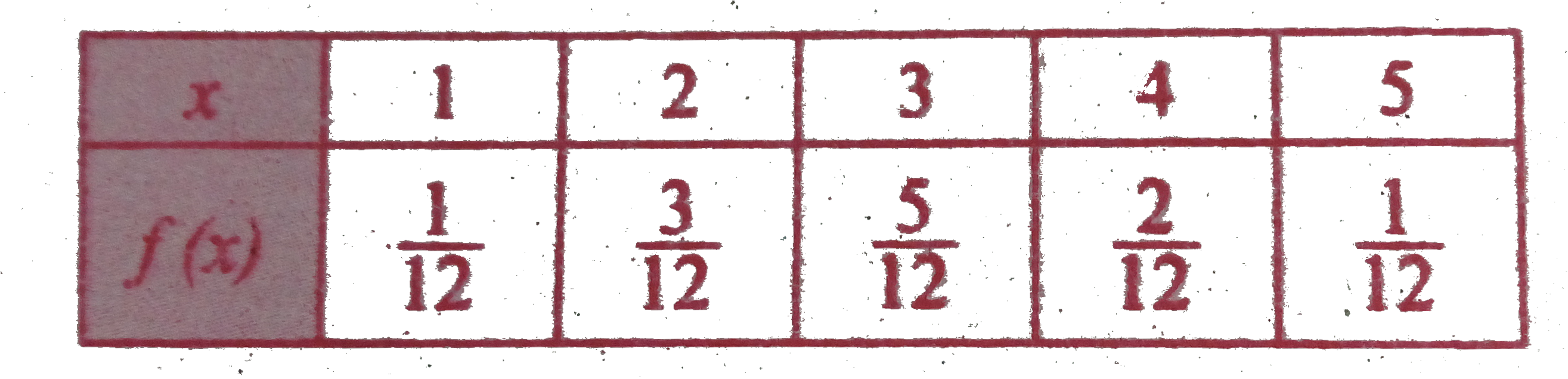 Find
Find
P(X≤3)07:37View SolutionFind the rpobability mass function f(x) of the discrete random variable X whose cumulative distribution function f(x) is given by
⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0−∞<x<−20.3−2≤x<−10.45−1≤x<00.70≤x<111≤x<∞
Also find P(x<0)03:08View Solution

