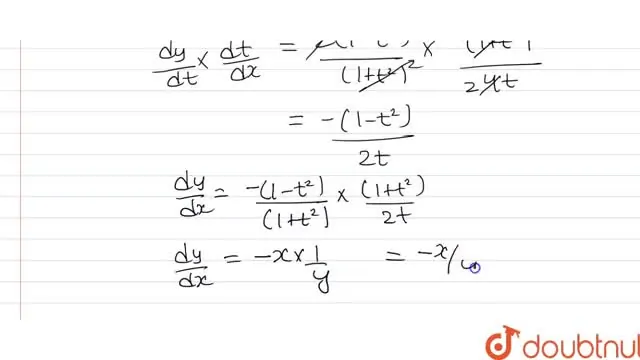If x=1−t21+t2 and y=2t1+t2, then dydx is equal to
A
−yx
B
yx
C
−xy
D
xy
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for If x=(1-t^(2))/(1+t^(2)) and y=(2t)/(1+t^(2)), then (dy)/(dx) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
If x=a(1+t21−t2) and y=2t1−t2 , find dydx
View SolutionIf x=a(1+t21−t2)andy=2t1−t2,f i n ddydx
View SolutionIf x=1−t21+t2 and y=2t1+t2, then: dydx∣∣∣t=1 is
View SolutionIf x=2t1+t2 and y=1−t21+t2, then dydx is equal to
View SolutionIf x=a(1−t21+t2),y=2bt1+t2,thendydx=
View SolutionConsider the parametric equation x=a(1−t2)1+t2 and y=2at1+t2
What is dydx equal to ?View SolutionIf x=1−t21+t2 and y=2at1+t2, then dydx=
View Solutionif x=1−t21+t2andy=2t1+t2, then dydx=
View SolutionIf x=1−t21+t2 and y=2t1+t2, prove that dydx+xy=0
View SolutionIf x=(1−t1+t) and y=(2t1+t), then d2ydx2 is
View Solution