If x=mx+c touches the parabola y2=4a(x+a), then c=am (b) c=am+am c=a+am (d) none of theseSolution in Tamil
c=1m
c=am+am
c=a+am
none of these
The correct Answer is:B
(2) The equation of tangent to the given parabola having slope m is
y=m(x+a)+am
ory=mx+am+am
Comparing (1) with y=mx+c, we have
c=am+am
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)
26 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)
41 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.7
9 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
4 Videos
Similar Questions
If the focus of the parabola x2−ky+3=0 is (0,2), then a values of k is (are) 4 (b) 6 (c) 3 (d) 2
View SolutionA tangent is drawn at any point P(t) on the parabola y2=8x and on it is takes a point Q(α,β) from which a pair of tangent QA and OB are drawn to the circle x2+y2=8. Using this information, answer the following questions :
The locus of circumcenter of ΔAQB id t=2 is
View SolutionIf the normal to the parabola y2=4ax at point t1 cuts the parabola again at point t2 , then prove that t22≥8.
View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionIf the number of ways in which a selection of 100 balls can be made out of 100 identical red balls, 100 identical blue balls and 100 identical white balls is
View SolutionIf x=mx+c touches the parabola y2=4a(x+a), then (a)c=am (b) c=am+am (c)c=a+am (d) none of these
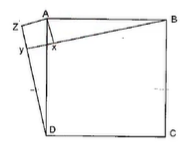
View SolutionIn Figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY=3 cm and AZ=2 cm, then BY=
(a) 5cm
(b) 6cm
(c) 7cm
(d) 8cm
View SolutionIf x^a y^b=e^m , x^c y^d=e^n ,Delta_1=|(m,b),(n,d)|,and Delta_2 =|(a,m),(c,n)| and Delta_3=|(a,b),(c,d)|, then the values of x and y are
View SolutionThe line y =m(x+a) + a/m touch the parabola y2=4a(x+a) for m
View SolutionIf the line y=mx+c touches the parabola y2=12(x+3) exactly for one value of m(m>0), then the value of c+mc−m is equal to
View Solutionxayb=cm,xc,yd=en,△1=[mbnd],△2=[amcn],△3=∣∣∣abcd∣∣∣ எனில் x மற்றும் y -ன் மதிப்புகள் முறையே,
View SolutionIf y=mx+c touches the parabola y2=4a(x+a), then (a)c=am (b) c=am+am (c)c=a+am (d) none of these
View SolutionThe lines which intersect the skew lines y=mx,z=c;y=−mx,z=−c and the x-axis lie on the surface: (a.) cz=mxy (b.) xy=cmz (c.) cy=mxz (d.) none of these
View SolutionThe lines which intersect the skew lines y=mx,z=c;y=−mx,z=−c and the x-axis lie on the surface
a. cz=mxy b. xy=cmz c. cy=mxz d. none of these
View SolutionIf y=mx+c touches the parabola y2=4a(x+a), then (a)c=am (b) c=am+am c=a+am (d) none of these
View SolutionXY is drawn parallel to the base BC of ΔABC cutting AB at X and AC at Y . If AB=4 BX and YC=2cm , then AY= (a) 2cm (b) 4cm (c) 6cm (d) 8cm
View Solution
