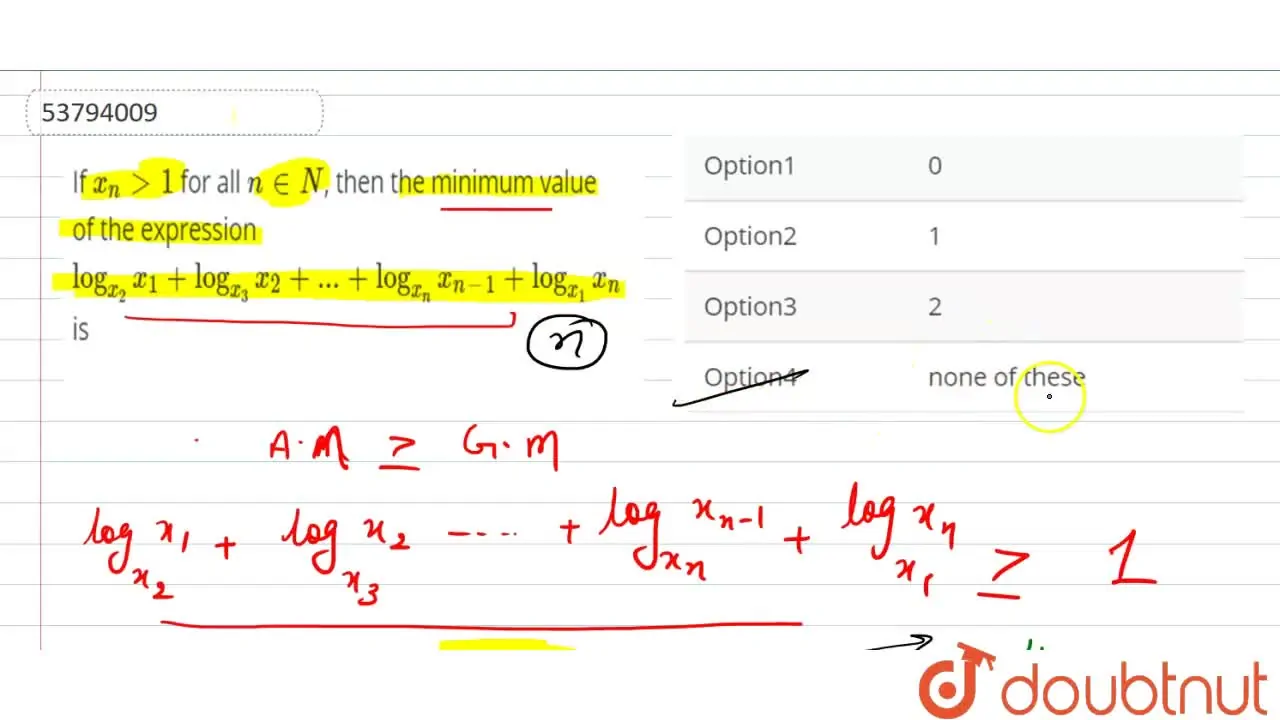
If xn>1 for all n∈N, then the minimum value of the expression
logx2x1+logx3x2+...+logxnxn−1+logx1xn is
0
1
2
none of these
The correct Answer is:D
Using A.M.≥G.M., we have
logx2x1+logx3x2+...+logxnxn−1+logx1xnn
≥(logx2x1.logx3x2....logx1xn)1/n
⇒ logx2x1+logx3x2+...+logx1xn≥n
Hence, the minimum value of the given expression is n and it attains this value when x1=x2=......=xn.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section 2 - Assertion Reason Type9videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section I - Mcqs37videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section II - Assertion Reason Type1videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Chapter Test29videos
HYPERBOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
Similar Questions
If xn>1 for all n∈N, then the minimum value of the expression
logx2x1+logx3x2+...+logxnxn−1+logx1xn isView SolutionIF x=198! then value of the expression 1log2x+1log3x+...+1log198x equals
View SolutionIf n=1983!, then the value of expression 1log2n+1log3n+1log4n.+......+1log1983n is equal to
View SolutionIf x=2000∏n=1n, then the value of the expression, 11(log)2x+1(log)3x++1(log)2000xis.
View SolutionlogxAn = ______
View SolutionThe least value of expression 2log10x−logx(1/100) for x>1 is:
View SolutionThe coeffiecient of xn in the expansion of logn(1+x) is
View SolutionFind the minimum value of logx1(x2−14)+logx2(x3−14)+.....+logx20(x1−14) over all x1,x2,....x20∈(14,1)
View Solution1log2(n)+1log3(n)+1log4(n)+.....+1log43(n) is equal to
View Solution1log2(n)+1log3(n)+1log4(n)+.....+1log43(n) is equals to
View Solution