If y=lotexxandz=logex, then d2ydz2+dydz=Solution in Telugu
e−z
2e−z
ze−z
−e−z
The correct Answer is:D
Step by step video, text & image solution for If y = (lot _(e) x)/(x) and z = log _(e) x, then (d ^(2) y)/(dz^(2)) + (dy)/(dz) = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:SET-2
Explore 4 Videos
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:SET-3
Explore 5 Videos
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:EXERCISE 1C
Explore 3 Videos
- DIFFERENTIAL EQUATIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIAL EQUATIONSExercise:Exercise 2
Explore 15 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:DIRECTION COSINES AND DIRECTION RATIOSExercise:EXERCISE 2 SET -2
Explore 3 Videos
Similar Questions
1.ifF(X)=1xthenf'(1)=A2.Iff(x)=x+1x+3thenf'(−1)=B3.Iff(x)=x2thenf'(1)=C4.Iff(x)=logxthenf'(3)=D
The ascending order of A,B,C ,D is
View SolutionMatch the following
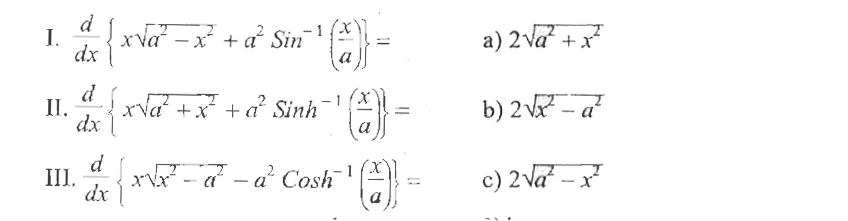
View SolutionThe function y=Sin−1(cosx) is not differentiable at
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
View SolutionIf y=esin−1x and z=e−cos−1x , prove that the value of dydz is independent of x.
View SolutionProve that ∫x0ezxe−z2dz=ex24∫x0ez24dz
View SolutionLet y=f(x)andx=1z. If d2ydx2=λz3dydz+z4d2ydz2, then the value of λ is
View SolutionIf x=1z,y=f(x) and d2ydx2=kz3dydz+z4d2ydz2, then the value of k is -
View SolutionIf y=sinx∘andz=log10x, then the value of dydz is -
View SolutionIf y=esin−1x and z=e−cos−1x, prove that the value of dydz independent of x.
View SolutionIf x=1z and y=f(x), then prove that,
d2fdx2=2z3dydz+z4d2ydz2
View SolutionPutting logx=z show that, x2d2ydx2=d2ydz2−dydz.
View Solutionx=1z এবং y=f(x) হলে দেখাও যে,
d2fdx2=2z3(dydz)+z4d2ydz2
View Solutionlogx=z ধরে দেখাও যে, x2d2ydx2=d2ydz2−dydz
View Solution
