If what is the value of when ?
The correct Answer is:
To solve the problem, we need to find the value of yz when p=2.5. We are given the equations:
1. y=2(2p−1)
2. z=p−2
Step 1: Substitute p=2.5 into the equation for y
y=2(2p−1)=2(2×2.5−1)
Step 2: Calculate 2×2.5
2×2.5=5
Step 3: Substitute back into the equation for y
y=2(5−1)=24
Step 4: Calculate 24
24=16
Step 5: Substitute p=2.5 into the equation for z
z=p−2=2.5−2
Step 6: Calculate 2.5−2
2.5−2=0.5
Step 7: Calculate yz
yz=160.5
Step 8: Simplify 160.5
To simplify 160.5, we can multiply both the numerator and the denominator by 2:
16×20.5×2=321=32
Final Answer
The value of yz when p=2.5 is 32.
---
2. z=p−2
Topper's Solved these Questions
Similar Questions
Knowledge Check
For positive integers y and z, if z2=y3andy2=16,what is the value of yz?
A0.2B0.4C0.5D2If p=√q+zr2+z, what is the value of z in terms of p, q, and r ?
Ap−r2√qp−1Bpr2−√qr2C√p+qrr2D√q−pr2p−1In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
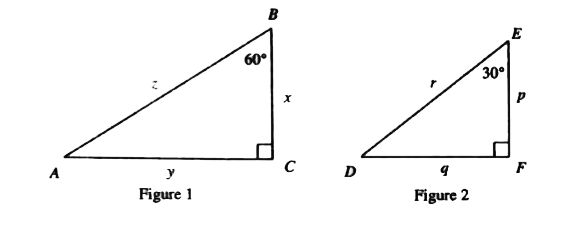 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
if p=4xyx+y, find the value of p+2xp−2x+p+2yp−2y.
View SolutionThe value of x + y + z is 15 if a, x, y, z, b are in A.P.
while the value of 1x+1y+1z+1zis53 if a, x, y, z, b are
in H.P. the value of a and b are
View SolutionIf y+(2p+1)x+3=0and8y−(2p−1)x=5 are mutually perpendicular, find the value of p.
View SolutionIf x,y,z are in H.P then the value of expression log(x+z)+log(x−2y+z)=
View SolutionIf distinct numbers x,y,zandp are chosen from the numbers -2, 2, 1/2, -1/3, what is the largest possible value of the expression x2yz−p ?
View Solution
