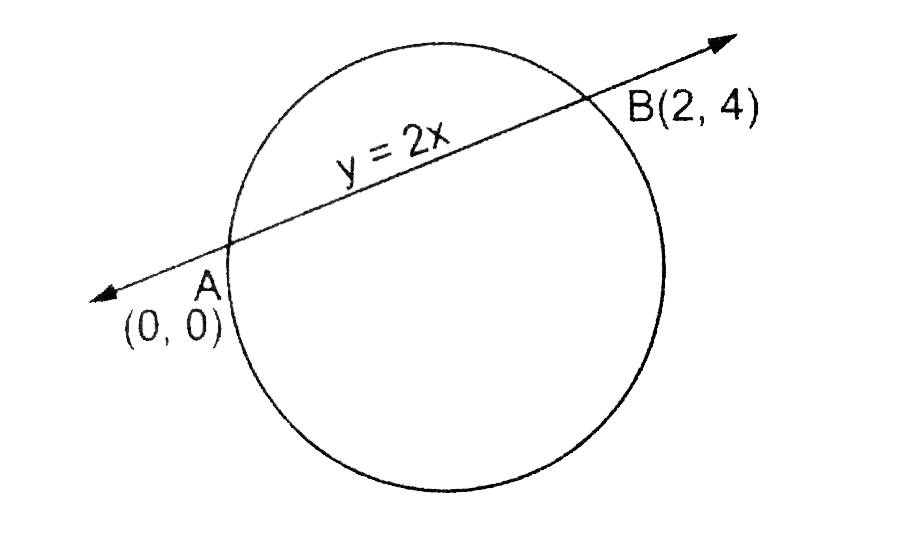
If $y = 2 x$ is a chord of the circle $x^{2} + y^{2} - 10 x = 0$ , find the equation of a circle with this chord as diameter.

Video Solution

Text Solution

Verified by Experts

The points of intersection of the given chord and the given circle are obtained by simultaneosly solving
$y = 2 x and x^{2} + y^{2} - 10 x = 0$
Putting $y = 2 x$ in $x^{2} + y^{2} - 10 x = 0$ , we get
$5 x^{2} - 10 x = 0 \Leftrightarrow 5 x (x - 2) = 0 \Leftrightarrow x = 0 or x = 2$
Now, $x = 0 \Rightarrow y = 0, and x = 2 \Rightarrow y = 4$
$∴$ the points of intersection of the given chord and the given circle are $A (0, 0) and B (2, 4)$
$∴$ the required equation of the circle with AB as diameter is
$(x - 0) (x - 2) + (y - 0) (y - 4) = 0$
$\Rightarrow x^{2} + y^{2} - 2 x - 4 y = 0$

|

Updated on:21/07/2023

Class 11 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-CIRCLE -EXERCISE 21 B

Home
Ask Doubt
Profile